设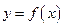 在
在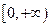 上有定义,对于给定的实数K,定义函数
上有定义,对于给定的实数K,定义函数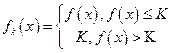 ,给出函数
,给出函数 ,若对于任意
,若对于任意 恒有
恒有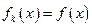 ,则( )
,则( )
| A.K的最小值为2 | B.K的最小值为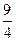 |
| C.K的最大值为2 | D.K的最大值为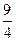 |
函数y=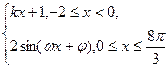 的图象如上图,则 ( )
的图象如上图,则 ( )
A.k= ,ω= ,ω=  ,φ= ,φ=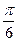 |
B.k= ,ω= ,ω= ,φ= ,φ= |
C.k  =- =- ,ω=2,φ= ,ω=2,φ=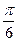 |
D.k=-2,ω=2,φ= |
已知 和
和 为互相垂直的单位向量,
为互相垂直的单位向量, ,
,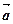 与
与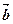 的夹角为锐角,则实数
的夹角为锐角,则实数 的取值范围是 ( )
的取值范围是 ( )
A. B
B .
. 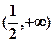
C.  D.
D.

如图,设 是单位圆和
是单位圆和 轴正半轴的交点,
轴正半轴的交点, 是单位圆上
是单位圆上 的两点,
的两点, 是坐标原点,
是坐标原点, ,
, .
.
(1)若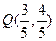 ,求
,求 的值;
的值;
(2)设函数 ,求
,求 的值域.
的值域.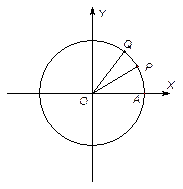
某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式 ,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出
,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出 该商品11千克。(I)
该商品11千克。(I) 求a的值;
求a的值;
(II)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大。
已知函数 图像上点
图像上点 处的切线与直线
处的切线与直线
平行(其中 ),
),
(I)求函数 的解析式;
的解析式;
(II)求函数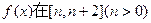 上的最小值;
上的最小值;
(III)对一切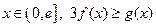 恒成立,求实数t的取值范围。
恒成立,求实数t的取值范围。
函数f(x)= 的零点所在的一个区间是( )
的零点所在的一个区间是( )
| A.(-2,-1) | B.(-1,0) | C.(0,1) | D.(1,2 ) ) |
右图是一个几何体的三视图,根据图中数据, 可得该几何体的表面积是( )
A. B.
B.
C .
. D.
D.

规定符号“ ”表示两个正实数之间的一种运算,即
”表示两个正实数之间的一种运算,即 =
= (
( 是正实数).已知1
是正实数).已知1 =3,则函数
=3,则函数 的值域是
的值域是
如图,平行四边形 中,
中, ,
, ,
, .将
.将 沿
沿 折起到
折起到 的位置,使平面
的位置,使平面 平面
平面 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求三棱锥 的侧面积.
的侧面积.