统计表明,某种型号的汽车在匀速行驶中每小时的耗油量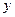 (升)关于行驶速度
(升)关于行驶速度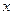 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: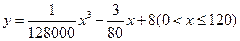 .已知甲、乙两地相距100千米
.已知甲、乙两地相距100千米
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
关于 的方程
的方程 ,给出下列四个命题:
,给出下列四个命题:
①存在实数 ,使得方程恰有2个不同实根;②存在实数
,使得方程恰有2个不同实根;②存在实数 ,使得方程恰有4个不同实根;
,使得方程恰有4个不同实根;
③存在实数 ,使得方程恰有5个不同实根;④存在实数
,使得方程恰有5个不同实根;④存在实数 ,使得方程恰有8个不同实根;
,使得方程恰有8个不同实根;
其中假命题的个数是 ( )
| A.0 | B.1 | C.2 | D.3 |
(本小题满分12分)设函数 (a为实数).
(a为实数).
(1)若a<0,用函数单调性定义证明: 在
在 上是增函数;
上是增函数;
(2)若a=0, 的图象与
的图象与 的图象关于直线y=x对称,求函数
的图象关于直线y=x对称,求函数 的解析式.
的解析式.