高中数学填空题

设 $f（x）$是定义在R上且周期为1的函数，在区间[0，1）上， $f（x）=\left\{\begin{array}{c}{x}^2，x\in D\\ x，x\notin D\end{array}\right.$ ，其中集合 $D=\left\{x\right|x=\frac{n-1}{n}，n\in N^{*}\}$，则方程 $f（x\mathit{）﹣}\mathit{lgx}=0$的解的个数是________．

在平面直角坐标系xOy中，A（﹣12，0），B（0，6），点P在圆O：x ²+y ²=50上．若 $\overrightarrow{\mathit{PA}}\cdot \overrightarrow{\mathit{PB}}\le 20$ ，则点P的横坐标的取值范围是________．

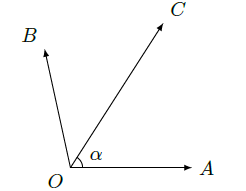
如图，在同一个平面内，向量 $\overrightarrow{\mathit{OA}}$， $\overrightarrow{\mathit{OB}}$， $\overrightarrow{\mathit{OC}}$的模分别为1，1， $\sqrt{2}$， $\overrightarrow{\mathit{OA}}$与 $\overrightarrow{\mathit{OC}}$的夹角为 $\alpha$，且 $\mathit{tan\alpha }=7$， $\overrightarrow{\mathit{OB}}$与 $\overrightarrow{\mathit{OC}}$的夹角为 $45°$ ．若 $\overrightarrow{\mathit{OC}}=\mathit{m}\overrightarrow{\mathit{OA}}+\mathit{n}\overrightarrow{\mathit{OB}}$ $（m，n\in R）$ ，则 $m+n=$ ________．

已知函数 $f（x）=x^3﹣2x+e^x﹣\frac{1}{e^x}$ ，其中e是自然对数的底数．若 $f（a﹣1）+f（2a^2）\le 0$ ．则实数a的取值范围是________．

某公司一年购买某种货物600吨，每次购买x吨，运费为6万元/次，一年的总存储费用为4x万元．要使一年的总运费与总存储费用之和最小，则x的值是________．

等比数列 $\left\{a_n\right\}$ 的各项均为实数，其前n项为S _n， 已知 $S_3=\frac{7}{4}$ ， $S_6=\frac{63}{4}$ ，则 $a_8=$ ________．

在平面直角坐标系 $\mathit{xOy}$ 中，双曲线 $\frac{x^2}{3}﹣y^2=1$ 的右准线与它的两条渐近线分别交于点P，Q，其焦点是 $F_1$ ， $F_2$ ， 则四边形 $F_{1}P{F}_{2}Q$ 的面积是________．

记函数 $f（x）=\sqrt{6+x-x^2}$ 定义域为D．在区间 $\left[﹣4，5\right]$ 上随机取一个数x，则 $x\in D$ 的概率是________．

如图，在圆柱 $O{ }_1{O}_{ 2}$内有一个球 $O$，该球与圆柱的上、下底面及母线均相切，记圆柱 $O_{ 1}{O}_{ 2}$的体积为 $V{ }_1$， 球 $O$的体积为 $V{ }_2$， 则 $\frac{V_1}{V_2}$ 的值是________．

若 $\mathit{tan}（\alpha ﹣\frac{\pi }{4}）=\frac{1}{6}$ ．则 $\mathit{tan\alpha }=$ ________．

如图是一个算法流程图：若输入x的值为 $\frac{1}{16}$ ，则输出y的值是________．

某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为200，400，300，100件．为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取60件进行检验，则应从丙种型号的产品中抽取________件．

已知复数 $z=（1+i\mathit{）（}1+2i）$ ，其中 $i$ 是虚数单位，则z的模是________．

已知集合A={1，2}，B={a，a ²+3}．若A∩B={1}，则实数a的值为________．

如图，圆形纸片的圆心为 $O$，半径为 $5cm$，该纸片上的等边三角形ABC的中心为O。D、E、F为圆O上的点， $△\mathit{DBC}$ ， $△\mathit{ECA}$ ， $△\mathit{FAB}$ 分别是以BC，CA，AB为底边的等腰三角形。沿虚线剪开后，分别以BC，CA，AB为折痕折起 $△\mathit{DBC}$ ， $△\mathit{ECA}$ ， $△\mathit{FAB}$ ，使得D、E、F重合，得到三棱锥。当 $△\mathit{ABC}$ 的边长变化时，所得三棱锥体积（单位： $cm{ }^3$）的最大值为_________.