高中数学填空题

已知直四棱柱ABCD–A₁B₁C₁D₁的棱长均为2，∠BAD=60°．以 $D_1$为球心， $\sqrt{5}$为半径的球面与侧面BCC₁B₁的交线长为________．

某中学开展劳动实习，学生加工制作零件，零件的截面如图所示． O为圆孔及轮廓圆弧 AB所在圆的圆心， A是圆弧 AB与直线 AG的切点， B是圆弧 AB与直线 BC的切点，四边形 DEFG为矩形， BC⊥ DG，垂足为 C，tan∠ ODC= $\frac{3}{5}$ ， $\mathit{BH}\parallel \mathit{DG}$ ， EF=12 cm， DE=2 cm， A到直线 DE和 EF的距离均为7 cm，圆孔半径为1 cm，则图中阴影部分的面积为________cm ²．

将数列{2n–1}与{3n–2}的公共项从小到大排列得到数列{a_n}，则{a_n}的前n项和为________．

斜率为 $\sqrt{3}$的直线过抛物线C：y²=4x的焦点，且与C交于A，B两点，则 $\left|\mathit{AB}\right|$=________．

设有下列四个命题：

p ₁：两两相交且不过同一点的三条直线必在同一平面内.

p ₂：过空间中任意三点有且仅有一个平面.

p ₃：若空间两条直线不相交，则这两条直线平行.

p ₄：若直线 l $\subset$ 平面 α，直线 m⊥平面 α，则 m⊥ l.

则下述命题中所有真命题的序号是__________.

① $p_1\wedge p_4$   ② $p_1\wedge p_2$   ③ $\neg p_2\vee p_3$   ④ $\neg p_3\vee \neg p_4$

设复数 $z_1$， $z_2$满足 $\left|z_1\right|=\left|z_2\right|=2$， $z_1+z_2=\sqrt{3}+i$，则 $|z_1-z_2|$=__________.

4名同学到3个小区参加垃圾分类宣传活动，每名同学只去1个小区，每个小区至少安排1名同学，则不同的安排方法共有__________种.

如图，在三棱锥 P- ABC的平面展开图中， AC=1， $\mathit{AB}=\mathit{AD}=\sqrt{3}$ ， AB⊥ AC， AB⊥ AD，∠ CAE=30°，则cos∠ FCB=______________.

设 $a,b$为单位向量，且 $|\vec{a}+\vec{b}|=1$，则 $|\vec{a}-\vec{b}|=$______________.

已知直四棱柱ABCD–A₁B₁C₁D₁的棱长均为2，∠BAD=60°．以 $D_1$为球心， $\sqrt{5}$为半径的球面与侧面BCC₁B₁的交线长为________．

某中学开展劳动实习，学生加工制作零件，零件的截面如图所示． O为圆孔及轮廓圆弧 AB所在圆的圆心， A是圆弧 AB与直线 AG的切点， B是圆弧 AB与直线 BC的切点，四边形 DEFG为矩形， BC⊥ DG，垂足为 C，tan∠ ODC= $\frac{3}{5}$ ， $\mathit{BH}\parallel \mathit{DG}$ ， EF=12 cm， DE=2 cm， A到直线 DE和 EF的距离均为7 cm，圆孔半径为1 cm，则图中阴影部分的面积为________cm ²．

在平面直角坐标系xOy中，已知 $P\left(\frac{\sqrt{3}}{2}，0\right)$，A，B是圆C： $x^2+(y-\frac{1}{2}{)}^2=36$上的两个动点，满足 $\mathit{PA}=\mathit{PB}$，则△PAB面积的最大值是__________．

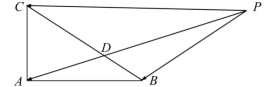
在△ ABC中， $\mathit{AB}=4，\mathit{AC}=3，\angle \mathit{BAC}=90°，$ D在边 BC上，延长 AD到 P，使得 AP=9，若 $\overrightarrow{\mathit{PA}}=m\overrightarrow{\mathit{PB}}+(\frac{3}{2}-m)\overrightarrow{\mathit{PC}}$ （ m为常数），则 CD的长度是________．

已知 $5x^2{y}^2+y^4=1(x,y\in R)$，则 $x^2+y^2$的最小值是_______．

设{a_n}是公差为d的等差数列，{b_n}是公比为q的等比数列．已知数列{a_n+b_n}的前n项和 $S_n=n^2-n+2^n-1(n\in N^{+})$，则d+q的值是_______．