高中数学填空题

      ．

对于函数，有下列4个命题：
①任取，都有恒成立；
②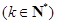，对于一切恒成立；
③函数有3个零点；
④对任意，不等式恒成立，则实数的取值范围是．
则其中所有真命题的序号是         ．

将长度为的线段分成段，每段长度均为正整数，并要求这段中的任意三段都不能构成三角形．例如，当时，只可以分为长度分别为1,1,2的三段，此时的最大值为3；当时，可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段，此时的最大值为4．则：
（1）当时，的最大值为________；
（2）当时，的最大值为________．

一环保部门对某处的环境状况进行了实地测量，据测定，该处的污染指数等于附近污染源的污染强度与该处到污染源的距离之比．已知相距30km的A，B两家化工厂(污染源)的污染强度分别为1和4，它们连线上任意一点处的污染指数等于两化工厂对该处的污染指数之和．现拟在它们之间的连线上建一个公园，为使两化工厂对其污染指数最小，则该公园应建在距A化工厂          公里处．

某个几何体的三视图如图所示，（其中正视图中的圆弧是半径为2的半圆），则该几何体的表面积为            ．

某程序框图如图所示，判断框内为“？”，为正整数，若输出的，则判断框内的________；

若，满足约束条件，则的最大值为        ．

在直角坐标平面内，以坐标原点为极点、轴的非负半轴为极轴建立极坐标系，已知点的极坐标为，曲线的参数方程为（为参数），则点到曲线上的点的距离的最小值为         ．

如图，已知是⊙的切线，是切点，直线交⊙于两点，是的中点，连接并延长交⊙于点，若，则      ．

将长度为的线段分成段，每段长度均为正整数，并要求这段中的任意三段都不能构成三角形．例如，当时，只可以分为长度分别为1,1,2的三段，此时的最大值为3；当时，可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段，此时的最大值为4．则：
（1）当时，的最大值为________；（2）当时，的最大值为________．

物体以速度（的单位：，的单位：）在一直线上运动，在此直线上
与物体出发的同时，物体在物体的正前方处以（的单位：，的单位：）的速度与同向运动，则两物体相遇时物体运动的距离为________．

设，则___ ____．

函数的图象为，如下结论中正确的是__________（写出所有正确结论的编号）．
①图象关于直线对称；
②图象关于点对称；
③函数在区间内是增函数；
④由的图象向右平移个单位长度可以得到图象

已知函数的值域是，则实数的取值范围是________________．

如图，一矩形铁皮的长为8cm，宽为5cm，在四个角上截去四个相同的小正方形，制成一个无盖的小盒子，则小正方形的边长为            时，盒子容积最大？。