已知P={x|x2﹣8x﹣20≤0},S={x|1﹣m≤x≤1+m}
(1)是否存在实数m,使x∈P是x∈S的充要条件,若存在,求出m的取值范围;
(2)是否存在实数m,使x∈P是x∈S的必要条件,若存在,求出m的取值范围.
已知公差不为零的等差数列{an},若a1=1,且a1,a2,a5成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=2n,求数列{an+bn}的前n项和Sn.
学校从参加高二年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及各组频数如下:
[40,50),2;[50,60),3;[60,70),14;[70,80),15;[80,90),12;[90,100],4.
| 分组 |
频数 |
频率 |
| [40,50) |
2 |
0.04 |
| [50,60) |
3 |
0.06 |
| [60,70) |
14 |
0.28 |
| [70,80) |
15 |
0.30 |
| [80,90) |
A |
B |
| [90,100] |
4 |
0.08 |
| 合计 |
C |
D |
(1)在给出的样本频率分布表中,求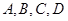 的值;
的值;
(2)估计成绩在80分以上(含80分)学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在[90,100]的学生中选两位同学,共同帮助成绩在[40,50)中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.
样本频率分布表如下:
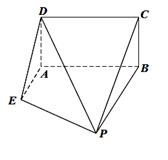
如图,已知矩形 所在平面垂直于直角梯形
所在平面垂直于直角梯形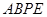 所在平面于直线
所在平面于直线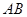 ,且
,且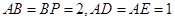 ,
,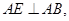 且
且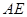 ∥
∥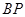 .
.
(Ⅰ)设点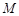 为棱
为棱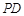 中点,求证:
中点,求证: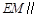 平面
平面 ;
;
(Ⅱ)线段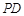 上是否存在一点
上是否存在一点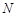 ,使得直线
,使得直线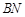 与平面
与平面 所成角的正弦值等于
所成角的正弦值等于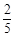 ?若存在,试确定点
?若存在,试确定点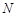 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.