(本小题满分12分)
在△ABC中,∠ACB=90°, ∠BAC=30°,AB的垂直平分线分别交AB,AC于D、E(图一),沿DE将△ADE折起,使得平面ADE⊥ 平面BDEC(图二),
(1)若F是AB的中点,求证: CF∥平面ADE;
CF∥平面ADE;
(2)P是AC上任意一点,求证:平面ACD⊥ 平面PBE ;
;
(3)P是AC上一点,且AC⊥ 平面PBE,求二面角P—BE—C的大小.
(本小题满分12分)
在△ABC中,角A,B,C所对的边分别为a,b,c 且 ,a=1,b=2,
,a=1,b=2,
(1)求C和c;
(2)P为△ABC内任一点(含边界),点P到三边距离之和为d,设P到AB,BC距离分别为x,y,用x,y表示d并求d的取值范围.
(本小题满分12分)
甲、乙、丙三台机床各自独立的加工同一种零件,已知甲、乙、丙三台机床加工的零件是一等品的概率分别为0.7、0.6、0.8,乙、丙两台机床加工的零件数相等,甲机床加工的零件数是乙机床加工的零件数的二倍.
(1)从甲、乙、丙加工的零件中各取一件检验,求至少有一件一等品的概率;
(2)将三台机床加工的零件混合到一起,从中任意的抽取一件检验,求它是一等品的概率;
(3)将三台机床加工的零件混合到一起,从中任意的抽取4件检验,其中一等品的个数记为X,求EX.
(本小题共14分)
已知椭圆 的焦点是
的焦点是 ,
, ,点
,点 在椭圆上且满足
在椭圆上且满足 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设直线 与椭圆
与椭圆 的交点为
的交点为 ,
, .
.
(i)求使 的面积为
的面积为 的点
的点 的个数;
的个数;
(ii)设 为椭圆上任一点,
为椭圆上任一点, 为坐标原点,
为坐标原点, ,求
,求 的值.
的值.
(本小题共14分)
设 是正数组成的数列,其前
是正数组成的数列,其前 项和为
项和为 ,且对于所有的正整数
,且对于所有的正整数 ,有
,有 .
.
(I) 求 ,
, 的值;
的值;
(II) 求数列 的通项公式;
的通项公式;
(III)令 ,
, ,
, (
( ),求
),求 的前20项和
的前20项和 .
.
(本小题共13分)
已知函数 .
.
(Ⅰ)当 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)若 在区间
在区间 上是减函数,求实数
上是减函数,求实数 的取值范围.
的取值范围.
(本小题共13分)
口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5.甲先摸出一个球,记下编号为 ,放回袋中后,乙再摸一个球,记下编号为
,放回袋中后,乙再摸一个球,记下编号为 .
.
(Ⅰ)求“ ”的事件发生的概率;
”的事件发生的概率;
(Ⅱ)若点 落在圆
落在圆 内,则甲赢,否则算乙赢,这个游戏规则公平吗?试说明理由.
内,则甲赢,否则算乙赢,这个游戏规则公平吗?试说明理由.
(本小题共13分)
已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中标出的数据,
(Ⅰ)求这个组合体的体积;
(Ⅱ)若组合体的底部几何体记为 ,其中
,其中 为正方形.
为正方形.
(i)求证: ;
;
(ii)求证: 为棱
为棱 上一点,求
上一点,求 的最小值.
的最小值.

(本小题共13分)
如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30 ,相距10海里C处的乙船.
,相距10海里C处的乙船.
(Ⅰ)求处于C处的乙船和遇险渔船间的距离;
(Ⅱ)设乙船沿直线 方向前往
方向前往 处救援,其方向与
处救援,其方向与 成
成 角,
角,
求 (x∈
(x∈ )的值域.
)的值域.
(本小题满分12分)
已知A、B分别为曲线C: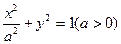 与x轴的左右两个交点,直线l过点B且x轴垂直,M为l上的一点,连结AM交曲线C于点T。
与x轴的左右两个交点,直线l过点B且x轴垂直,M为l上的一点,连结AM交曲线C于点T。
(I)当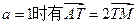 ,求点T坐标;
,求点T坐标;
(II)点M在x轴上方,若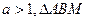 的面积为2,当
的面积为2,当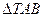 的面积的最大值为
的面积的最大值为 时,求曲线C的离心率e的取值范围。
时,求曲线C的离心率e的取值范围。
(本大题满分12分)
给出定义在 上的三个函数:
上的三个函数: ,已知
,已知 处取极值.
处取极值.
(I)确定函数 的单调性;
的单调性;
(II)求证:当 成立.
成立.
(III)把函数 的图象向上平移6个单位得到函数
的图象向上平移6个单位得到函数 的图象,试确定函数
的图象,试确定函数 的零点个数,并说明理由。
的零点个数,并说明理由。
(本小题满分12分)
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(I)求出该几何体的体积;
(II)求证:EM∥平面ABC;
|
(III)试问在棱DC上是否存在点N,使NM⊥平面 ?若存在,确定点N的位置;
?若存在,确定点N的位置; 若不存在,请说明理由.
若不存在,请说明理由.
(本小题满分12分)从某学校高三年级共800名男生中随机抽取50名测量身高,据测量被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组 、第二组
、第二组 ;…第八组
;…第八组 ,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
(I)求第六组、第七组的频率并补充完整频率分布直方图;
(II)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为 ,求满足
,求满足 的事件概率;
的事件概率;
(III)从最后三组中任取3名学生参加学校篮球队,用 表示从第八组中取到的人数,求
表示从第八组中取到的人数,求 的分布列及其数学期望。
的分布列及其数学期望。
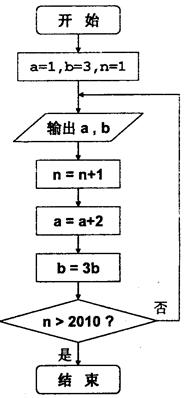
根据如图所示的程序框图,将输出的a,b值依次分别记为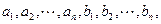 其中
其中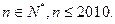
(I)分别求数列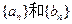 的通项公式;
的通项公式;
(II)令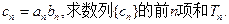
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题 满分8分.
满分8分.
从数列 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列 的一个子数列.
的一个子数列.
设数列 是一个首项为
是一个首项为 、公差为
、公差为
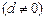 的无穷等差数列.
的无穷等差数列.
(1)若 ,
, ,
,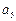 成等
成等 比数列,求其公比
比数列,求其公比 .
.
(2)若 ,从数列
,从数列 中取出第2项、第6项作为一个等比数列的第1项、第2项,试问该数列是否为
中取出第2项、第6项作为一个等比数列的第1项、第2项,试问该数列是否为 的无穷等比子数列,请说明理由.
的无穷等比子数列,请说明理由.
(3)若 ,从数列
,从数列 中取出第1项、第
中取出第1项、第
 项(设
项(设 )作为一个等比数列的第1项、第2项,试问当且仅当
)作为一个等比数列的第1项、第2项,试问当且仅当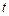 为何值时,该数列为
为何值时,该数列为 的无穷等比子数列,请说明理由.
的无穷等比子数列,请说明理由.