海南省高三五校联考数学(理)
设全集U={1,2,3,4,5,6,7,8},集合A={2,4,
5,7},B={1,4,7,8},那么如图所示的阴影部分
所表示的集合是 ( )
| A.{3,6} | B.{4,7} |
| C.{1,2,4,5,7,8} | D.(1,2,3,5,6,8) |
复数z满足 在复平面内所对应的点的坐标是( )
在复平面内所对应的点的坐标是( )
| A.(1,—3) | B.(—1,3) | C.(—3,1) | D.(3,—1) |
下列说法错误的是 ( )
A.如果命题“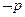 ”与命题“ ”与命题“ ”都是真命题,那么命题q一定是真命题; ”都是真命题,那么命题q一定是真命题; |
B.命题“若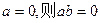 ”的否命题是:“若 ”的否命题是:“若 ”; ”; |
C.若命题p: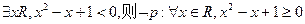 ; ; |
D.“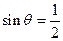 ”是“ ”是“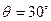 ”的充分不必要条件 ”的充分不必要条件 |
设l、m、n表示不同的直线, 、
、 、
、 表示不同的平面,给出下列四个命题:
表示不同的平面,给出下列四个命题:
①若 ;
;
②若 ;
;
③若 ;
;
④若
其中正确命题的个数是 ( )
| A.1 | B.2 | C.3 | D.4 |
如图,设D是图中所示的矩形区域,E是D内函数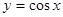 图象上方的点构成的区域。向D中随机投
图象上方的点构成的区域。向D中随机投
一点,则该点落入E(阴影部分)中的概率为( )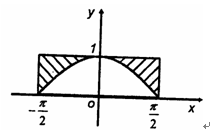
A.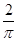 |
B.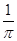 |
C. |
D.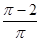 |
如图,正六边形ABCDEF的两个项点,A、D为双曲线的两个焦点,其余4个顶点都在双曲线上,则该双曲线的离心率是( )
A. B.
B.
C. D.
D.

已知a,b,c分别为△ABC的三个内角A,B,C的对边,向量 ,则△ABC周长的最小值为 ( )
,则△ABC周长的最小值为 ( )
A. |
B. |
C. |
D. |
在棱长为1的正方形ABCD—A1B1C1D1的底面A1B1C1D1内取一点E,使AE与AB、AD所成的角都是60°,则线段AE的长为 ( )
A. B.
B. C.
C. D.
D.
观察下列各式并填空:1=1,2+3+4=9,3+4+5+6+7= ,4+5+6+7+8+9+10=49,…,由此可归纳出 = 。
= 。
某企业职工的月工资数统计如下:
| 月工资数(元) |
10000 |
8000 |
5500 |
2500 |
1600 |
1200 |
900 |
600 |
500 |
| 得此工资人数 |
1 |
3 |
3 |
8 |
20 |
35 |
45 |
3 |
2 |
经计算,该企业职工工资的平均值为1565元,众数是900元,中位数是 元。如何选取该企业的月工资代表数呢?企业法人主张用平均值,职工代表主张用众数,监管部门主张用中位数。
请你站在其中一立场说明理由: 。
(本小题满分12分)从某学校高三年级共800名男生中随机抽取50名测量身高,据测量被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组 、第二组
、第二组 ;…第八组
;…第八组 ,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
(I)求第六组、第七组的频率并补充完整频率分布直方图;
(II)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为 ,求满足
,求满足 的事件概率;
的事件概率;
(III)从最后三组中任取3名学生参加学校篮球队,用 表示从第八组中取到的人数,求
表示从第八组中取到的人数,求 的分布列及其数学期望。
的分布列及其数学期望。
(本小题满分12分)
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(I)求出该几何体的体积;
(II)求证:EM∥平面ABC;
|
(III)试问在棱DC上是否存在点N,使NM⊥平面 ?若存在,确定点N的位置;
?若存在,确定点N的位置; 若不存在,请说明理由.
若不存在,请说明理由.
(本小题满分12分)
设F1、F2分别是椭圆 的左、右焦点。
的左、右焦点。
(I)若P是第一象限内该椭圆上的一点,且 ,求点P的坐标;
,求点P的坐标;
(II)设过定点M(0,2)的直线l与椭圆交于不同的两点A、B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围。
(本大题满分12分)
给出定义在 上的三个函数:
上的三个函数: ,已知
,已知 处取极值.
处取极值.
(I)确定函数 的单调性;
的单调性;
(II)求证:当 成立.
成立.
(III)把函数 的图象向上平移6个单位得到函数
的图象向上平移6个单位得到函数 的图象,试确定函数
的图象,试确定函数 的零点个数,并说明理由。
的零点个数,并说明理由。
选做题:请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题记分
22.(本小题满分10分)选修4—1几何证明选讲
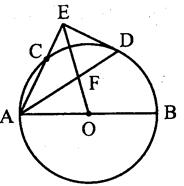
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F。
(I)求证:DE是⊙O的切线;
(II)若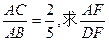 的值.
的值.
23.(本小题满分10分)选修4—2坐标系与参数方程
设直角坐标系原点与极坐标极点重合,x轴正半轴与极轴重合,若已知曲线C的极坐标方程为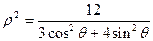 ,点F1、F2为其左、右焦点,直线l的参数方程为
,点F1、F2为其左、右焦点,直线l的参数方程为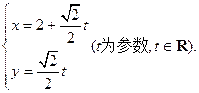
(I)求直线l的普通方程和曲线C的直角坐标方程;
(II)求曲线C上的动点P到直线l的最大距离。
24.(本小题满分10分)选修4—5不等式选讲
对于任意的实数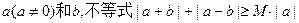 恒成立,记实数M的最大值是m。
恒成立,记实数M的最大值是m。
(1)求m的值;
(2)解不等式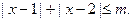
 成等差数列,则S5= ( )
成等差数列,则S5= ( ) ( )
( )

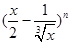 的展开式中,只有第5项的二项式系数最大,则展开式中常数项是( )
的展开式中,只有第5项的二项式系数最大,则展开式中常数项是( ) ,设
,设 的取值范围是 ( )
的取值范围是 ( ) 的焦点为F,准线与y轴的交点为M,N为抛物线上的一点,且
的焦点为F,准线与y轴的交点为M,N为抛物线上的一点,且 。
。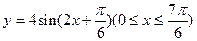 的图象与一条平行于x轴的直线有三个交点,其横坐标分别为
的图象与一条平行于x轴的直线有三个交点,其横坐标分别为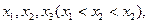
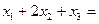 。
。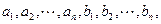 其中
其中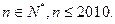
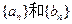 的通项公式;
的通项公式;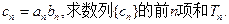

 粤公网安备 44130202000953号
粤公网安备 44130202000953号