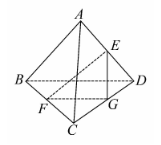
若函数 对定义域中任意
对定义域中任意 均满足
均满足 ,则称函数
,则称函数 的图象关于点
的图象关于点 对称.
对称.
(1)已知函数 的图象关于点
的图象关于点 对称,求实数m的值;
对称,求实数m的值;
(2)已知函数 在
在 上的图象关于点
上的图象关于点 对称,且当
对称,且当 时,
时, ,求函数
,求函数 在
在 上的解析式;
上的解析式;
(3)在(1)(2)的条件下,当 时,若对任意实数
时,若对任意实数 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
设有关于 的一元二次方程
的一元二次方程 .
.
(1)若 是从
是从 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(2)若 是从区间
是从区间 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
已知函数f(x)=xln x,g(x)=(-x2+ax-3)ex(a为实数).
(1)当a=5时,求函数y=g(x)在x=1处的切线方程;
(2)求f(x)在区间 (t>0)上的最小值.
(t>0)上的最小值.
已知中心在坐标原点的椭圆E的长轴的一个端点是抛物线y2=4 x的焦点,且椭圆E的离心率是
x的焦点,且椭圆E的离心率是 .
.
(1)求椭圆E的方程;
(2)过点C(-1,0)的动直线与椭圆E相交于A,B两点.若线段AB的中点的横坐标是 ,求直线AB的方程.
,求直线AB的方程.
已知向量m=(sin ωx+ cosωx,1),n=(2cos ωx,-
cosωx,1),n=(2cos ωx,- )(ω>0),函数f(x)=m·n的两条相邻对称轴间的距离为
)(ω>0),函数f(x)=m·n的两条相邻对称轴间的距离为 .
.
(1)求函数f(x)的单调递增区间;
(2)当x∈[- ,
, ] 时,求f(x)的值域.
] 时,求f(x)的值域.
已知 ,命题
,命题 “
“ 均成立”,命题
均成立”,命题 “函数
“函数 定义域为R”.
定义域为R”.
(1)若命题 为真命题,求实数
为真命题,求实数 的取值范围;
的取值范围;
(2)若命题 为真命题,命题
为真命题,命题 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健产品的收益与投资成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比. 已知投资1万元时两类产品的收益分别为 万元和0.5万元.
万元和0.5万元.
(1)分别写出两类产品的收益与投资的函数关系;
(2)该家庭有20万元资金,全部用于理财投资,问,怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
四面体ABCD中,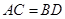 ,E、F分别是AD、BC的中点,且
,E、F分别是AD、BC的中点,且 ,
,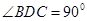 ,求证:
,求证: 平面ACD.
平面ACD.