若函数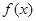 对定义域中任意
对定义域中任意 均满足
均满足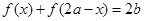 ,则称函数
,则称函数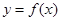 的图象关于点
的图象关于点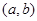 对称.
对称.
(1)已知函数 的图象关于点
的图象关于点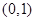 对称,求实数m的值;
对称,求实数m的值;
(2)已知函数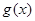 在
在 上的图象关于点
上的图象关于点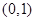 对称,且当
对称,且当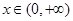 时,
时,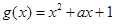 ,求函数
,求函数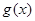 在
在 上的解析式;
上的解析式;
(3)在(1)(2)的条件下,当 时,若对任意实数
时,若对任意实数 ,恒有
,恒有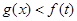 成立,求实数
成立,求实数 的取值范围.
的取值范围.
推荐套卷
若函数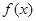 对定义域中任意
对定义域中任意 均满足
均满足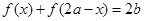 ,则称函数
,则称函数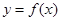 的图象关于点
的图象关于点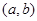 对称.
对称.
(1)已知函数 的图象关于点
的图象关于点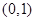 对称,求实数m的值;
对称,求实数m的值;
(2)已知函数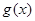 在
在 上的图象关于点
上的图象关于点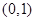 对称,且当
对称,且当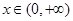 时,
时,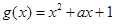 ,求函数
,求函数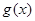 在
在 上的解析式;
上的解析式;
(3)在(1)(2)的条件下,当 时,若对任意实数
时,若对任意实数 ,恒有
,恒有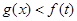 成立,求实数
成立,求实数 的取值范围.
的取值范围.