(本小题满分12分)已知二次函数f(x)=ax2+bx+c.
(1)若f(-1)=0,试判断函数f(x)零点的个数;
(2)是否存在a,b,c∈R,使f(x)同时满足以下条件:
①对任意x∈R,f(-1+x)=f(-1-x),且f(x)≥0;
②对任意x∈R,都有0≤f(x)-x≤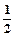 (x-1)2.若存在,求出a,b,c的值;若不存在,请说
(x-1)2.若存在,求出a,b,c的值;若不存在,请说
明理由。
(3)若对任意x1、x2∈R且x1<x2,f(x1)≠f(x2),试证明:存在x0∈(x1,x2),使f(x0)=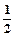 [f(x1)+f(x2)]成立。
[f(x1)+f(x2)]成立。
相关知识点
推荐套卷
 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,有
时,有 (其中
(其中 为自然对数的底,
为自然对数的底, ).
).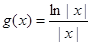 ,
,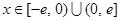 ,求证:当
,求证:当 时,
时, ;
;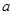 ,使得当
,使得当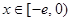 时,
时,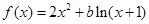 ,其中
,其中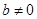 .
.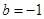 时,求在曲线
时,求在曲线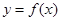 上一点
上一点 处的切线方程;
处的切线方程;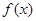 的极值点。
的极值点。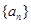 的前
的前 项和为
项和为 ,且
,且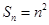 .数列
.数列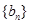 为等比数列,且
为等比数列,且 ,
, .
.  满足
满足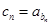 ,求数列
,求数列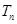 .
.
 的值;
的值; .
. ,求
,求 的最大值及此时相应的
的最大值及此时相应的 的值;
的值; 、b、c分别为角A、B、C的对边,若
、b、c分别为角A、B、C的对边,若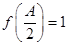 ,b =l,
,b =l,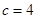 ,求
,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号