（本小题满分12分）
设函数f（x）=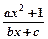
是奇函数（a,b,c都是整数）且f（1）=2,f（2）<3
（1）求a,b,c的值；
（2）当x<0，f（x）的单调性如何？用单调性定义证明你的结论。
（3）当x>0时，求函数f（x）的最小值。
相关试题
如图所示，四棱锥
的底面是边长为１的正方形，
，
，
点是棱
的中点。
（１）求证
；
（２）求异面直线
与
所成的角的大小；
（３）求面
与面
所成二面角的大小。
（第18题图）
的定义域为集合
，函数
的定义域为集合
。
时，求
；
求实数
的值。
上，求使
取得最大值和最小值的点
的坐标．
是椭圆的两个焦点，
为椭圆上一点，
．
的面积只与椭圆的短轴长有关．推荐套卷
（本小题满分12分）
设函数f（x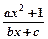）=是奇函数（a,b,c都是整数）且f（1）=2,f（2）<3
（1）求a,b,c的值；
（2）当x<0，f（x）的单调性如何？用单调性定义证明你的结论。
（3）当x>0时，求函数f（x）的最小值。
如图所示，四棱锥的底面是边长为１的正方形，，，点是棱的中点。
（１）求证；
（２）求异面直线与所成的角的大小；
（３）求面与面所成二面角的大小。
（第18题图）
粤公网安备 44130202000953号