（本小题满分12分）
已知点(x, y) 在曲线C上，将此点的纵坐标变为原来的2倍,对应的横坐标不变,得到的点满足方程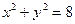
；定点M(2,1)，平行于OM的直线
在y轴上的截距为m(m≠0),直线与曲线C交于A、B两个不同点.
(1)求曲线
的方程；
(2)求m的取值范围.
相关试题
，
．
及
的值；
的锐角
．
，且
均为钝角，求
的值．
．
=（x，3）．
，求x的值；
，求x的值．
，
，其中
．设函数
．
的最小正周期；
上的最大值和最小值．推荐套卷
（本小题满分12分）
已知点(x, y) 在曲线C上，将此点的纵坐标变为原来的2倍,对应的横坐标不变,得到的点满足方程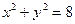；定点M(2,1)，平行于OM的直线在y轴上的截距为m(m≠0),直线与曲线C交于A、B两个不同点.
(1)求曲线的方程；
(2)求m的取值范围.
粤公网安备 44130202000953号