选修4-1:几何证明选讲
如图,直线 为圆的切线,切点为
为圆的切线,切点为 ,点
,点 在圆上,
在圆上, 的角平分线
的角平分线 交圆于点
交圆于点 垂直
垂直 交圆于点
交圆于点 .
.
(1)证明:
(2)设圆的半径为1, ,延长
,延长 交
交 于点
于点 ,求
,求 外接圆的半径.
外接圆的半径.
已知椭圆 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)设 ,过点
,过点 作与
作与 轴不重合的直线
轴不重合的直线 交椭圆
交椭圆 于
于 两点,连接
两点,连接 分别交直线
分别交直线 于
于 两点,若直线
两点,若直线 的斜率分别为
的斜率分别为 ,试问:
,试问: 是否为定值?若是,求出该定值,若不是,请说明理由.
是否为定值?若是,求出该定值,若不是,请说明理由.
如图(1),在三角形ABC中,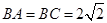 ,
,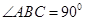 ,点O、M、N分别为线段的中点,将ABO和MNC分别沿BO,MN折起,使平面ABO与平面CMN都与底面OMNB垂直,如图(2)所示.
,点O、M、N分别为线段的中点,将ABO和MNC分别沿BO,MN折起,使平面ABO与平面CMN都与底面OMNB垂直,如图(2)所示.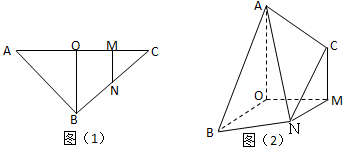
(1)求证: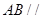 平面CMN;
平面CMN;
(2)求点M到平面CAN的距离.
选修4-4:坐标系与参数方程
在直角坐标系 中,圆
中,圆 的参数方程为
的参数方程为 ,(
,( 为参数),以
为参数),以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆 的极坐标方程;
的极坐标方程;
(2)直线 的极坐标方程是
的极坐标方程是 ,射线
,射线 与圆
与圆 的交点为
的交点为 ,与直线
,与直线 的交点为
的交点为 ,求线段
,求线段 的长.
的长.