(14分) 如图,已知底角为450的等腰梯形ABCD,底边BC长为7cm,腰长为 ,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式。
,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式。 
已知:函数 对一切实数
对一切实数 都有
都有
 成立,且
成立,且 .
.
(1)求 的值。
的值。
(2)求 的解析式。
的解析式。
(3)已知 ,设P:当
,设P:当 时,不等式
时,不等式 恒成立;Q:当
恒成立;Q:当 时,
时, 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的 的集合记为
的集合记为 ,满足Q成立的
,满足Q成立的 的集合记为
的集合记为 ,求
,求 ∩
∩ (
( 为全集)。
为全集)。
已知集合A= ,B={x|2<x<10},C={x|x<a},全集为实数集R.
,B={x|2<x<10},C={x|x<a},全集为实数集R.
(1)求A∪B, ; (2)如果A∩C≠φ,求a的取值范围.
; (2)如果A∩C≠φ,求a的取值范围.
(本小题满分14分) 函数f(x)的图象是如下图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0).
(1)求f(x)的解析式
(2)定义函数g(x)=f(x)·(x-1),求函数g(x)的最大值。
(本题满分13分)二次函数 的图像顶点为
的图像顶点为 ,且图象在
,且图象在 轴上截得线段长为
轴上截得线段长为 .
.
(1)求函数 的解析式;
的解析式;
(2)令
①若函数 在
在 上是单调增函数,求实数
上是单调增函数,求实数 的取值范围;
的取值范围;
②求函数 在
在 的最小值.
的最小值.
(本小题满分12分)某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如下图所示.

(1)上表是年龄的频数分布表,求正整数 的值;
的值;
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
(本小题满分12分)如图为一简单组合体,其底面ABCD为正方形, 平面
平面 ,
, ,且
,且
 .
.
(1)求四棱锥B-CEPD的体积;
(2)求证: 平面
平面 .
.
(本小题满分12分)某高校在2011年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85), 第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
(ⅰ)已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙同时进入第二轮面试的概率;
(ⅱ)学校决定在这6名学生中随机抽取2名学生接受考官D的面试,设第4组中有 名学生被考官D面试,求
名学生被考官D面试,求 的分布列和数学期望.
的分布列和数学期望.
已知函数 ∈R).
∈R).
(1)若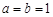 ,求
,求 点(
点(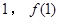 )处的切线方程;
)处的切线方程;
(2)设a≤0,求 的单调区间;
的单调区间;
(3)设a<0,且对任意的 ,
, ≤
≤ ,试比较
,试比较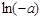 与
与 的大小.
的大小.