高中数学解答题

（本题小满分10分）设命题：函数在上单调递增；：关于的方程的解集只有一个子集．若“”为真，“”为假，求实数的取值范围．

设函数，
（1）当，解不等式，；
（2）若的解集为，，求证：

（本小题满分10分）选修4-l：几何证明选讲在ABC中，D是AB边上一点，ACD的外接圆交BC于点E，AB= 2BE

（1）求证：BC= 2BD；
（2）若CD平分ACB，且AC =2，EC =1，求BD的长

己知函数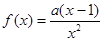，其中 
（1）求函数的单调区间；
（2）若直线x-y-l=0是曲线y=的切线，求实数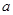的值；
（3）设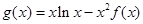，求g(x)在区间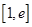上的最大值（其中e为自然对数的底数）

设数列满足
（1）求数列的通项公式；
（2）令，求数列的前n项和

如图，直三棱柱中，D，E分别是AB，的中点

（1）证明：；
（2）设，求三棱锥的体积

己知长方体的三条棱长分别为a、b、c，其外接球的半径为
（1）求长方体体积的最大值：
（2）设，求的最大值

己知抛物线的顶点M到直线(t为参数)的距离为1
（1）求m；
（2）若直线与抛物线相交于A，B两点，与y轴交于N点，求的值．

（本小题满分10分）选修4-l：几何证明选讲如图，是ABC的外接圆，D是的中点，BD 交AC于E

（1）求证：：
（2）若，O到AC的距离为1，求的半径

已知函数(d为常数）
（1）当对，求单调区间；
（2）若函数在区间(0，1)上无零点，求a的最大值．

己知四棱锥P-ABCD，其中底面ABCD为矩形侧棱PA底面ABCD，其中BC=2,AB=2PA=6，
M,N为侧棱PC上的两个三等分点，如图所示：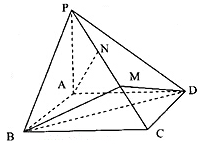

（1）求证：AN∥平面MBD；
（2）求二面角B-PC-A的余弦值．

设X为随机变量，从棱长为a的正方体,的八个顶点中任取四个点，当四点共面时，X=0；当四点不共面时，X的值为四点组成的四面体的体积．
（1）求概率P(X=0)；
（2）求X的分布列，并求其数学期望E(X)．

（本题满分分）已知，函数.（的图像连续不断）
（1）求的单调区间；
（2）当时，证明：存在，使；
（3）若存在均属于区间的，且，使，证明

（本题满分分）设数列的前项和为，已知，，.
（1）求数列的通项公式；
（2）证明：对一切正整数，有.

设向量，，.
（1）若，求的值；
（2）设函数，求的最大值．