高中数学解答题

(1)已知，且为第三象限角，求的值
(2)已知，计算  的值

如图：平面四边形ABCD中，，，,沿对角线将折起，使面面,

(1)求证：面；
(2)求点到面的距离.

已知关于的不等式，
（1）当时解不等式；
（2）如果不等式的解集为空集，求实数的范围.

已知不等式的解集为
（1）求的值；
（2）解不等式

如图，已知四棱锥的底面是菱形,平面,,点为的中点.

（Ⅰ）求证:平面;
（Ⅱ）求二面角的正切值.

已知f(x)=
（1）求f()，f[f(－)]值；
（2）若f(x)=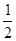，求x值；
（3）作出该函数简图；
（4）求函数值域.

(本小题满分12分)
已知函数.
(Ⅰ)若，，求函数f(x)的值；  
(Ⅱ)求函数f(x)的最小正周期和值域.

(本小题满分12分)如图，在四棱锥P—ABCD中，底面是边长为的菱形，且∠BAD＝120°，且PA⊥平面ABCD，PA＝，M，N分别为PB，PD的中点．

(Ⅰ)证明：MN∥平面ABCD；
(Ⅱ) 过点A作AQ⊥PC，垂足为点Q，求二面角A—MN—Q的平面角的余弦值．

已知函数
（1）求的单调递减区间；
（2）若，证明：.

求函数的极大值。

. (本小题满分12分)
已知函数.
(1)若函数在处取得极值,且曲线在点处的切线与直线平行,求和的值;
(2)若,试讨论函数的单调性.

(本小题满分12分)
已知等差数列满足：，，的前n项和为．
（Ⅰ）求通项公式及前n项和； 
（Ⅱ）令=(nN^*)，求数列的前n项和．

已知关于的不等式：的整数解有且仅有一个值为2．
（1）求整数的值；（2）在（1）的条件下，解不等式：． 

（本题8分）已知直线l₁：2x－y＋2＝0与l₂：x＋2y－4＝0，点P(1, m)．
（Ⅰ）若点P到直线l₁, l₂的距离相等，求实数m的值；
（Ⅱ）当m＝1时，已知直线l经过点P且分别与l₁, l₂相交于A, B两点，若P恰好
平分线段AB，求A, B两点的坐标及直线l的方程．

(本小题满分12分) 已知函数的图像经过点，曲线在点处的切线恰好与直线垂直．
（I）求实数的值；
（Ⅱ）若函数在区间上单调递增，求实数的取值范围．