已知函数f(x)= ,其中a>0.
,其中a>0.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
已知曲线C :
: (t为参数), C
(t为参数), C :
: (
( 为参数)。
为参数)。
(Ⅰ)化C ,C
,C 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(Ⅱ)若C 上的点P对应的参数为
上的点P对应的参数为 ,Q为C
,Q为C 上的动点,求
上的动点,求 中点
中点 到
到
直线 (t为参数)距离的最小值。
(t为参数)距离的最小值。
已知抛物线的顶点在原点,它的准线过双曲线 ,(
,( )的一个焦点,且这条准线与双曲线的两个焦点连线互相垂直,又抛 物线与双曲线交于点
)的一个焦点,且这条准线与双曲线的两个焦点连线互相垂直,又抛 物线与双曲线交于点 ,求抛物线和双曲线的方程.
,求抛物线和双曲线的方程.
(本小题满分14分) 已知函数
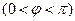 其图象过点
其图象过点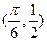 .
.
(I) 求 的值;
的值;
(Ⅱ) 将函数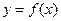 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数 的图象,求函数
的图象,求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
.(本小题满分12分) 设关于 的一元二次方程
的一元二次方程 .
.
(I) 若 是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个
是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个
数,求上述方程有实根的概率;
(Ⅱ) 若 是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程
是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程
有实根的概率.
(本小题满分12分) 己知函数 ,
, (其中
(其中 ,
, ,
, )的图象与
)的图象与 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为 ,且图象上一个最低点为
,且图象上一个最低点为
(I) 求 的解析式。
的解析式。
(Ⅱ) 求函教 单调递减区间.
单调递减区间.
(本题满分12分) 袋中有大小、形状相同的红、黑球各一个,现依次有放回地随机摸取
3次,每次摸取一个球.
(I) 试问;一共有多少种不同的结果? 请列出所有可能的结果;
(II) 若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率.
(本题满分12分) 已知 顶点的直角坐标分别为
顶点的直角坐标分别为 ,
, ,
,
(I) 若 ,求
,求 的值;
的值;
(II) 若 ,求
,求 的值。
的值。
(III) 若 是钝角,求
是钝角,求 的取值范围.
的取值范围.
(本小题满分13分)
已知
(1)若 ,函数
,函数 在其定义域内是增函数,求
在其定义域内是增函数,求 的取值范围;
的取值范围;
(2)当 时,证明:函数
时,证明:函数 只有一个零点;
只有一个零点;
(3)若 的图象与
的图象与 轴交于
轴交于 两点,AB中点为
两点,AB中点为 ,求证:
,求证:
(本小题满分13分)
旅游部门开发一种旅游纪念品,每件产品的成本是15元,销售价是20元,月平均销售 件。通过改进工艺,产品的成本不变,质量和技术含量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件。通过改进工艺,产品的成本不变,质量和技术含量提高,市场分析的结果表明,如果产品的销售价提高的百分率为 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为 。记改进工艺后,旅游部门销售该纪念品的月平均利润是
。记改进工艺后,旅游部门销售该纪念品的月平均利润是 (元)。
(元)。
(1)写出 与
与 的函数关系式;
的函数关系式;
(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大。
(本小题满分13分)
已知 是二次函数,不等式
是二次函数,不等式 的解集是(0,5),且
的解集是(0,5),且 在区间[-1,4]上的最大值是12。
在区间[-1,4]上的最大值是12。
(1)求 的解析式;
的解析式;
(2)是否存在自然数 ,使得方程
,使得方程 在区间
在区间 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。