(本题满分12分)已知函数 在定义域
在定义域 上是奇函数,又是减函数。
上是奇函数,又是减函数。
(Ⅰ)证明:对任意的 ,有
,有
(Ⅱ)解不等式 。
。
(本小题9分)等差数列{an}不是常数列,a5=10,且a5,a7,a10是某一等比数列{bn}的第1,2,3项,(1)求数列{an}的第20项,(2)求数列{bn}的通项公式。
(本小题满分14分) 如果对于函数 的定义域内的任意
的定义域内的任意 成立,那么就称函数
成立,那么就称函数 是定义域上的“平缓函数”.
是定义域上的“平缓函数”.
(1)判断函数 ,
, 是否是 “平缓函数”?
是否是 “平缓函数”?
(2)若函数 是闭区间
是闭区间 上的“平缓函数”,且
上的“平缓函数”,且 .证明:对任意的
.证明:对任意的 都有
都有 .
.
(本小题满分12分) 所对的边分别为
所对的边分别为 ,且
,且 .
.
(Ⅰ)求角A;
(Ⅱ)已知 求
求 的值.
的值.
(本题满分14分)已知集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}
(Ⅰ)若A B=[0,3],求实数m的值
B=[0,3],求实数m的值
(Ⅱ)若A CRB,求实数m的取值范围
CRB,求实数m的取值范围
如图,一辆汽车从O点出发,沿海岸一条直线公路以100千米/时的速度向东匀速行驶,汽车开动时,在O点南偏东方向距O点500千米且与海岸距离MQ为300千米的海上M处有一快艇,与汽车同时出发,要把一件重要的物品递送给这辆汽车的司机,问快艇至少须以多大的速度行驶,才能把物品递送到司机手中,并求快艇以最小速度行驶时的方向与OM所成的角.
已知函数
(1)求函 数
数 的定义域;
的定义域;
(2)求证:函数 是增函数;
是增函数;
(3)求函数 的最小值.
的最小值.
(本小题满分14分)已知椭圆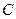 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,长轴长为
轴上,长轴长为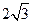 ,离心率为
,离心率为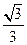 ,经过其左焦点
,经过其左焦点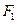 的直线
的直线 交椭圆
交椭圆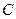 于
于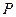 、
、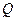 两点(I)求椭圆
两点(I)求椭圆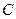 的方程;
的方程;
(II)在 轴上是否存在一点
轴上是否存在一点 ,使得
,使得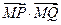 恒为常数?若存在,求出
恒为常数?若存在,求出 点的坐标和这个常数;若不存在,说明理由.
点的坐标和这个常数;若不存在,说明理由.