如图，一辆汽车从O点出发，沿海岸一条直线公路以100千米/时的速度向东匀速行驶，汽车开动时，在O点南偏东方向距O点500千米且与海岸距离MQ为300千米的海上M处有一快艇，与汽车同时出发，要把一件重要的物品递送给这辆汽车的司机，问快艇至少须以多大的速度行驶，才能把物品递送到司机手中，并求快艇以最小速度行驶时的方向与OM所成的角.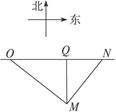
相关试题
满足
；
的值；（2）求
的值
，M是BC边上的中点.
底面ABCD，E是PC的中点．
，已知不论
为何实数恒有
.
；
；
的最大值为8，求
的值.
，
，且
.
的最值；
的值，使
相关知识点
推荐套卷
如图，一辆汽车从O点出发，沿海岸一条直线公路以100千米/时的速度向东匀速行驶，汽车开动时，在O点南偏东方向距O点500千米且与海岸距离MQ为300千米的海上M处有一快艇，与汽车同时出发，要把一件重要的物品递送给这辆汽车的司机，问快艇至少须以多大的速度行驶，才能把物品递送到司机手中，并求快艇以最小速度行驶时的方向与OM所成的角.
粤公网安备 44130202000953号