已知双曲线 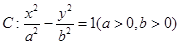 的左、右焦点分别是
的左、右焦点分别是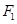 、
、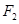 过
过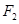 垂直x轴的直线与双曲线C的两渐近线的交点分别是M、N,若
垂直x轴的直线与双曲线C的两渐近线的交点分别是M、N,若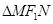 为正三角形,则该双曲线的离心率为( )
为正三角形,则该双曲线的离心率为( )
A.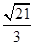 |
B. |
C.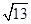 |
D.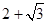 |
若函数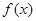 满足
满足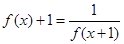 ,当x∈[0,1]时,
,当x∈[0,1]时,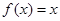 ,若在区间(-1,1]上,
,若在区间(-1,1]上, 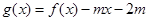 有两个零点,则实数m的取值范围是
有两个零点,则实数m的取值范围是
A.0<m≤ |
B.0<m< |
C. <m≤l <m≤l |
D. <m<1 <m<1 |
德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数
被称为狄利克雷函数,其中 为实数集,
为实数集, 为有理数集,则关于函数
为有理数集,则关于函数 有如下四个命题:
有如下四个命题:
① ; ②函数
; ②函数 是偶函数;
是偶函数;
③任取一个不为零的有理数 ,
, 对任意的
对任意的 恒成立;
恒成立;
④存在三个点 ,使得
,使得 为等边三角形.
为等边三角形.
其中真命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
已知关于x的方程: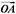 ·x2+
·x2+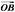 ·2x+
·2x+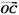 =0(x∈R),其中点C为直线AB上一点,O是直线AB外一点,则下列结论正确的是 ( )
=0(x∈R),其中点C为直线AB上一点,O是直线AB外一点,则下列结论正确的是 ( )
| A.点C在线段AB上 |
| B.点C在线段AB的延长线上且点B为线段AC的中点 |
| C.点C在线段AB的反向延长线上且点A为线段BC的中点 |
| D.以上情况均有可能 |
设[x]表示不超过x的最大整数(如[2]=2,[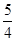 ]=1),对于给定的n
]=1),对于给定的n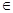 N*,定义
N*,定义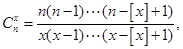 x
x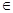
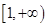 ,则当x
,则当x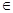
 时,函数
时,函数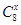 的值域是( )
的值域是( )
A.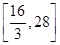 |
B.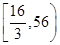 |
C.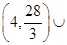 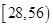 |
D.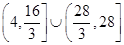 |
已知中心在原点、焦点在x轴上的椭圆C1与双曲线C2有共同的焦点,设左右焦点分别为F1,F2,P是C1与C2在第一象限的交点,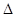 PF1F2是以PF1为底边的等腰三角形,若椭圆与双曲线的离心率分别为e1,e2,则e1·e2的取值范围是( )
PF1F2是以PF1为底边的等腰三角形,若椭圆与双曲线的离心率分别为e1,e2,则e1·e2的取值范围是( )
A.(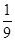 ,+ ,+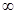 ) ) |
B.(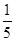 ,+ ,+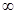 ) ) |
C.(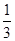 ,+ ,+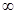 ) ) |
D.(0,+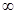 ) ) |
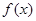 是定义在
是定义在 上的奇函数,其图象如图所示,令
上的奇函数,其图象如图所示,令 ,则下列关于函数
,则下列关于函数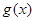 的叙述正确的是
的叙述正确的是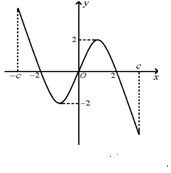
A.若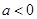 ,则函数 ,则函数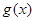 的图象关于原点对称 的图象关于原点对称 |
B.若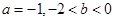 ,则方程 ,则方程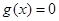 有大于2的实根 有大于2的实根 |
C.若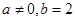 ,则方程 ,则方程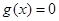 有两个实根 有两个实根 |
D.若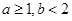 ,则方程 ,则方程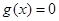 有两个实根 有两个实根 |
已知函数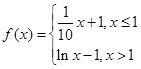 ,则方程
,则方程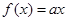 恰有两个不同实数根时,实数
恰有两个不同实数根时,实数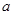 的取值范围是( )
的取值范围是( )
A.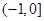 |
B.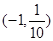 |
C.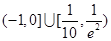 |
D.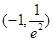 |
过双曲线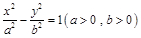 的一个焦点作实轴的垂线,交双曲线于
的一个焦点作实轴的垂线,交双曲线于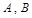 两点,若线段
两点,若线段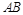 的长度恰等于焦距,则双曲线的离心率为( )
的长度恰等于焦距,则双曲线的离心率为( )
A.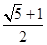 |
B.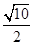 |
C.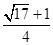 |
D.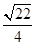 |
过椭圆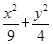 =1上一点M作圆x2+y2=2的两条切线,点A,B为切点.过A,B的直线l与x轴、y轴分别交于P,Q两点,则△POQ的面积的最小值为( )
=1上一点M作圆x2+y2=2的两条切线,点A,B为切点.过A,B的直线l与x轴、y轴分别交于P,Q两点,则△POQ的面积的最小值为( )
A.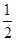 |
B.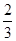 |
C.1 | D.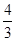 |
设点P在曲线y=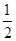 ex上,点Q在曲线y=ln(2x)上,则|PQ|的最小值为( ).
ex上,点Q在曲线y=ln(2x)上,则|PQ|的最小值为( ).
| A.1-ln 2 | B.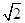 (1-ln 2) (1-ln 2) |
C.1+ln 2 | D.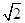 (1+ln 2) (1+ln 2) |
若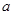 、
、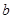 是方程
是方程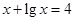 ,
,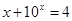 的解,函数
的解,函数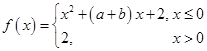 ,则关于
,则关于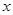 的方程
的方程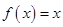 的解的个数是( )
的解的个数是( )
A.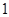 |
B. |
C.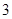 |
D.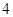 |
若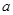 、
、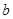 是方程
是方程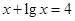 ,
,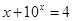 的解,函数
的解,函数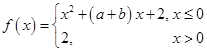 ,则关于
,则关于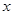 的方程
的方程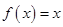 的解的个数是( )
的解的个数是( )
A. |
B. |
C.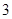 |
D.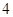 |