高考数学文复习二轮作业手册新课标·通用版限时集15讲练习卷
已知椭圆C: =1,直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )
=1,直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )
| A.[1,4) | B.[1,+∞) | C.[1,4)∪(4,+∞) | D.(4,+∞) |
与两圆x2+y2=1及x2+y2-8x+12=0都外切的圆的圆心在( )
| A.一个椭圆上 | B.双曲线的一支上 |
| C.一条抛物线上 | D.一个圆上 |
已知两定点A(1,1),B(-1,-1),动点P(x,y)满足 ·
· =
= ,则点P的轨迹是( )
,则点P的轨迹是( )
| A.圆 | B.椭圆 | C.双曲线 | D.拋物线 |
已知椭圆C1: =1与双曲线C2:
=1与双曲线C2: =1共焦点,则椭圆C1的离心率e的取值范围为( )
=1共焦点,则椭圆C1的离心率e的取值范围为( )
A. |
B. |
C.(0,1) | D. |
以抛物线y2=8x上的任意一点为圆心作圆与直线x+2=0相切,这些圆必过一定点,则这一定点的坐标是( )
| A.(0,2) | B.(2,0) |
| C.(4,0) | D.(0,4) |
过椭圆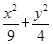 =1上一点M作圆x2+y2=2的两条切线,点A,B为切点.过A,B的直线l与x轴、y轴分别交于P,Q两点,则△POQ的面积的最小值为( )
=1上一点M作圆x2+y2=2的两条切线,点A,B为切点.过A,B的直线l与x轴、y轴分别交于P,Q两点,则△POQ的面积的最小值为( )
A.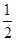 |
B.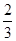 |
C.1 | D.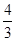 |
已知点A(2,1),抛物线y2=4x的焦点是F,若抛物线上存在一点P,使得|PA|+|PF|最小,则P点的坐标为( )
| A.(2,1) | B.(1,1) | C. |
D. |
过抛物线y2=x的焦点F的直线m的倾斜角θ≥ ,m交抛物线于A,B两点,且A点在x轴上方,则|FA|的取值范围是________.
,m交抛物线于A,B两点,且A点在x轴上方,则|FA|的取值范围是________.
已知E(2,2)是抛物线C:y2=2px上一点,经过点(2,0)的直线l与抛物线C交于A,B两点(不同于点E),直线EA,EB分别交直线x=-2于点M,N,则∠MON的大小为________.
如图所示,已知椭圆C: +y2=1,在椭圆C上任取不同两点A,B,点A关于x轴的对称点为A′,当A,B变化时,如果直线AB经过x轴上的定点T(1,0),则直线A′B经过x轴上的定点为________.
+y2=1,在椭圆C上任取不同两点A,B,点A关于x轴的对称点为A′,当A,B变化时,如果直线AB经过x轴上的定点T(1,0),则直线A′B经过x轴上的定点为________.
已知椭圆C: =1,过点M(2,0)且斜率不为0的直线交椭圆C于A,B两点.在x轴上若存在定点P,使PM平分∠APB,则P的坐标为________.
=1,过点M(2,0)且斜率不为0的直线交椭圆C于A,B两点.在x轴上若存在定点P,使PM平分∠APB,则P的坐标为________.
如图所示,已知抛物线方程为y2=4x,其焦点为F,准线为l,A点为抛物线上异于顶点的一个动点,射线HAE垂直于准线l,垂足为H,C点在x轴正半轴上,且四边形AHFC是平行四边形,线段AF和AC的延长线分别交抛物线于点B和点D.
(1)证明:∠BAD=∠EAD;
(2)求△ABD面积的最小值,并写出此时A点的坐标.
如图X15-3所示,已知圆C1:x2+(y-1)2=4和抛物线C2:y=x2-1,过坐标原点O的直线与C2相交于点A,B,定点M的坐标为(0,-1),直线MA,MB分别与C1相交于点D,E.
(1)求证:MA⊥MB;
(2)记△MAB,△MDE的面积分别为S1,S2,若 =λ,求λ的取值范围.
=λ,求λ的取值范围.
 =1(a>b>0)的两个焦点分别为F1,F2,离心率为
=1(a>b>0)的两个焦点分别为F1,F2,离心率为 ,且过点(2,
,且过点(2, ).
). 为定值.
为定值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号