已知椭圆C: =1(a>b>0)的两个焦点分别为F1,F2,离心率为
=1(a>b>0)的两个焦点分别为F1,F2,离心率为 ,且过点(2,
,且过点(2,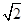 ).
).
(1)求椭圆C的标准方程;
(2)M,N,P,Q是椭圆C上的四个不同的点,两条都不和x轴垂直的直线MN和PQ分别过点F1,F2,且这两条直线互相垂直,求证: 为定值.
为定值.
推荐套卷
已知椭圆C: =1(a>b>0)的两个焦点分别为F1,F2,离心率为
=1(a>b>0)的两个焦点分别为F1,F2,离心率为 ,且过点(2,
,且过点(2,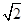 ).
).
(1)求椭圆C的标准方程;
(2)M,N,P,Q是椭圆C上的四个不同的点,两条都不和x轴垂直的直线MN和PQ分别过点F1,F2,且这两条直线互相垂直,求证: 为定值.
为定值.