函数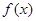 的定义域为
的定义域为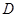 ,若满足:
,若满足:
①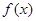 在
在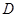 内是单调函数;
内是单调函数;
②存在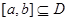 ,使
,使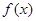 在
在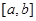 上的值域为
上的值域为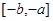 ,那么
,那么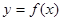 叫做对称函数.
叫做对称函数.
现有 是对称函数,那么
是对称函数,那么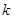 的取值范围是( )
的取值范围是( )
A.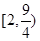 |
B.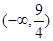 |
C.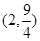 |
D.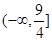 |
设函数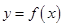 在区间
在区间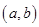 上的导函数为
上的导函数为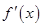 ,
,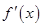 在区间
在区间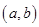 上的导函数为
上的导函数为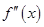 ,若区间
,若区间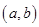 上
上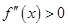 ,则称函数
,则称函数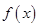 在区间
在区间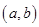 上为“凹函数”,已知
上为“凹函数”,已知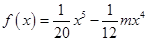
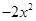 在
在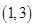 上为“凹函数”,则实数m的取值范围是( )
上为“凹函数”,则实数m的取值范围是( )
A.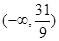 |
B.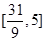 |
C.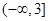 |
D.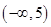 |
如图,在一个正方体内放入两个半径不相等的球 ,这两个球相外切,且球
,这两个球相外切,且球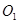 与正方体共顶点A的三个面相切,球
与正方体共顶点A的三个面相切,球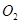 与正方体共顶点
与正方体共顶点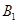 的三个面相切,则两球在正方体的面
的三个面相切,则两球在正方体的面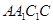 上的正投影是( )
上的正投影是( )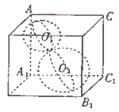

已知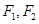 分别是双曲线
分别是双曲线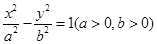 的左、右焦点,以坐标原点
的左、右焦点,以坐标原点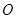 为圆心,
为圆心,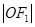 为半径的圆与双曲线在第一象限的交点为
为半径的圆与双曲线在第一象限的交点为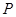 ,则当
,则当 的面积等于
的面积等于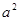 时,双曲线的离心率为 ( )
时,双曲线的离心率为 ( )
A.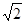 |
B. |
C.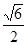 |
D.2 |
已知抛物线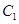 :
:
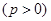 的焦点与双曲线
的焦点与双曲线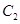 :
: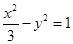 的右焦点的连线交
的右焦点的连线交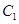 于第一象限的点
于第一象限的点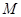 ,若
,若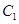 在点
在点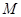 处的切线平行于
处的切线平行于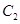 的一条渐近线,则
的一条渐近线,则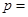 ( )
( )
A.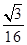 |
B.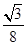 |
C.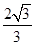 |
D.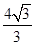 |
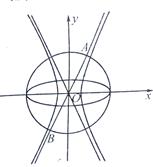
如图,已知椭圆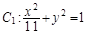 ,双曲线
,双曲线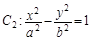 (a>0,b>0),若以C1的长轴为直径的圆与C2的一条渐近线交于A,B两点,且C1与该渐近线的两交点将线段AB三等分,则C2的离心率为( )
(a>0,b>0),若以C1的长轴为直径的圆与C2的一条渐近线交于A,B两点,且C1与该渐近线的两交点将线段AB三等分,则C2的离心率为( )
| A.5 | B.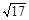 |
C.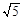 |
D.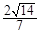 |
已知双曲线 与抛物线
与抛物线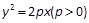 有一个共同的焦点F, 点M是双曲线与抛物线的一个交点, 若
有一个共同的焦点F, 点M是双曲线与抛物线的一个交点, 若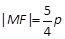 , 则此双曲线的离心率等于( ).
, 则此双曲线的离心率等于( ).
A.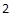 |
B.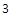 |
C.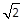 |
D.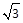 |
已知函数f(n)= ,且an=f(n)+f(n+1),则a1+a2+a3+…+a2014等于( )
,且an=f(n)+f(n+1),则a1+a2+a3+…+a2014等于( )
| A.-2013 | B.-2014 | C.2013 | D.2014 |
如图,已知双曲线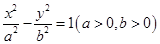 的左、右焦点分别为
的左、右焦点分别为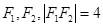 ,P是双曲线右支上的一点,
,P是双曲线右支上的一点, 轴交于点A,
轴交于点A,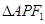 的内切圆在
的内切圆在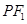 上的切点为Q,若
上的切点为Q,若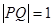 ,则双曲线的离心率是
,则双曲线的离心率是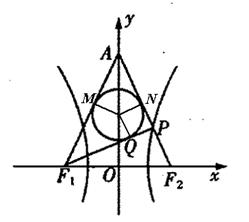
| A.3 | B.2 | C.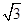 |
D.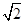 |
将两个顶点在抛物线 上,另一个顶点是此抛物线焦点的正三角形个数记为 ,则()
| A. | B. | C. | D. |
设直线与函数
的图像分别交于点
,则当
达到最小时
的值为()
| A. | 1 | B. |
|
C. |
|
D. |
|