定义在R上的函数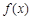 满足
满足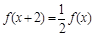 ,当
,当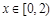 时,
时,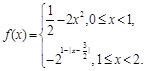 函数
函数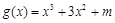 .若
.若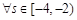 ,
,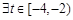 ,不等式
,不等式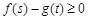 成立,则实数m的取值范围是( )
成立,则实数m的取值范围是( )
A.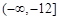 |
B. |
C.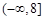 |
D.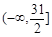 |
已知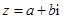
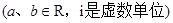 ,
, ,定义:
,定义: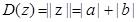 ,
,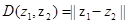 .给出下列命题:
.给出下列命题:
(1)对任意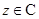 ,都有
,都有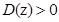 ;
;
(2)若 是复数
是复数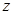 的共轭复数,则
的共轭复数,则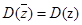 恒成立;
恒成立;
(3)若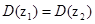
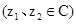 ,则
,则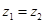 ;
;
(4)对任意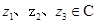 ,结论
,结论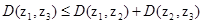 恒成立,则其中真命题是[答]( ).
恒成立,则其中真命题是[答]( ).
| A.(1)(2)(3)(4) | B.(2)(3)(4) | C.(2)(4) | D.(2)(3) |
已知函数 是定义域为
是定义域为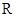 的偶函数. 当
的偶函数. 当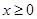 时,
时,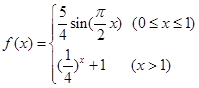 若关于
若关于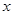 的方程
的方程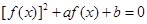 (
(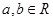 ),有且仅有6个不同实数根,则实数
),有且仅有6个不同实数根,则实数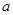 的取值范围是( )
的取值范围是( )
A.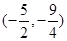 |
B.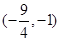 |
C.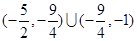 |
D.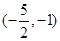 |
抛物线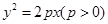 的焦点为
的焦点为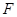 ,准线为
,准线为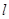 ,
,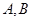 是抛物线上的两个动点,且满足
是抛物线上的两个动点,且满足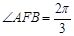 .设线段
.设线段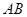 的中点
的中点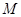 在
在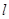 上的投影为
上的投影为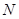 ,则
,则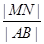 的最大值是
的最大值是
A.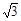 |
B.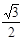 |
C.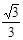 |
D.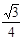 |
(理科做)如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F且EF=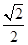 ,则下列结论中错误的是 ( ).
,则下列结论中错误的是 ( ).
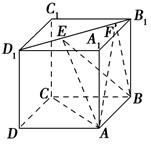
A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A-BEF的体积为定值
D.异面直线AE,BF所成的角为定值
(文科做)对于三次函数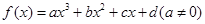 ,给出定义:设
,给出定义:设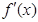 是函数
是函数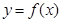 的导数,
的导数,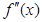 是
是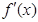 的导数,若方程
的导数,若方程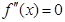 有实数解
有实数解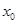 ,则称点
,则称点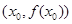 为函数
为函数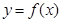 的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数
的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数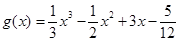 ,则
,则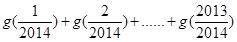 =( )
=( )
A.2011 B.2012 C.2013 D.2014
设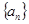 是等比数列,公比
是等比数列,公比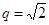 ,
,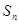 为
为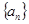 的前n项和。记
的前n项和。记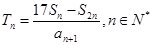 ,设
,设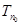 为数列
为数列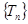 的最大项,则
的最大项,则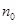 =( )
=( )
| A.3 | B.4 | C.5 | D.6 |
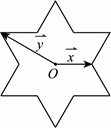
将一圆的六个等分点分成两组相间的三点﹐它们所构成的两个正三角形扣除内部六条线段后可以形成一正六角星﹐如图所示的正六角星是以原点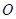 为中心﹐其中
为中心﹐其中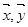 ,分别为原点
,分别为原点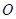 到两个顶点的向量﹒若将原点
到两个顶点的向量﹒若将原点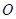 到正六角星12个顶点的向量﹐都写成为
到正六角星12个顶点的向量﹐都写成为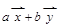 的形式﹐则
的形式﹐则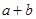 的最大值为( )
的最大值为( )
| A.2 | B.3 | C.4 | D.5 |
如图,PA垂直于圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E, F分别是点A在P B, P C上的射影,给出下列结论:
① ;②
;② ;③
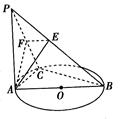
;③ ;④
;④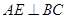 .正确命题的个数为( )
.正确命题的个数为( )
| A.1 | B.2 | C.3 | D.4 |
已知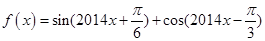 的最大值为
的最大值为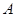 ,若存在实数
,若存在实数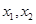 ,使得对任意实数x总有
,使得对任意实数x总有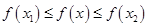 成立,则
成立,则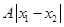 的最小值为( )
的最小值为( )
A.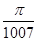 |
B.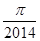 |
C.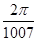 |
D.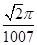 |
设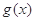 为
为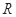 上不恒等于0的奇函数,
上不恒等于0的奇函数,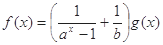 (
(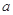 >0且
>0且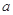 ≠1)为偶函数,则常数
≠1)为偶函数,则常数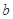 的值为( )
的值为( )
| A.2 | B.1 | C.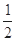 |
D.与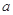 有关的值 有关的值 |