对于任意的两个实数对(a, b)和(c, d),规定(a, b)=(c, d)当且仅当a=c ,b=d;运算
“ ”为:
”为: ,运算“
,运算“ ”为:
”为: ,设
,设 ,若
,若
则 ( )
( )
A. |
B. |
C. |
D. |
设 ,定义运算"∧"和"∨"如下: , 若正数 、 、 、 满足 , ,则()
| A. | B. | C. | D. |
已知全集为 ,集合
,集合 ,那么集合
,那么集合 等于( )
等于( )
A. |
B. |
C. |
D. |
已知集合 ,
, 是集合
是集合 的非空子集,把集合
的非空子集,把集合 中的各元素之和记作
中的各元素之和记作 .
.
①满足 的集合
的集合 的个数为_____;②
的个数为_____;② 的所有不同取值的个数为_____.{本题第一空3分,第二空2分}
的所有不同取值的个数为_____.{本题第一空3分,第二空2分}
已知集合M={ },若对于任意
},若对于任意 ,存在
,存在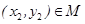 ,使得
,使得 成立,则称集合M是“垂直对点集”.给出下列四个集合:
成立,则称集合M是“垂直对点集”.给出下列四个集合:
①M={ }; ②M={
}; ②M={ };
};
③M={ }; ④M={
}; ④M={ }.
}.
其中是“垂直对点集”的序号是( )
| A.①② | B.②④ | C.①④ | D.②③ |
给定集合A={a1,a2,a3,……an}( ),定义ai+aj(
),定义ai+aj( )中所有不同值的个数为集合A元素和的容量,用L(A)表示。若A={2,4,6,8},则L(A)= ;若数列{an}是等差数列, 公差不为0,设集合A={a1,a2,a3,……am}(其中
)中所有不同值的个数为集合A元素和的容量,用L(A)表示。若A={2,4,6,8},则L(A)= ;若数列{an}是等差数列, 公差不为0,设集合A={a1,a2,a3,……am}(其中 ,m为常数),则L(A)关于m的表达式为 .
,m为常数),则L(A)关于m的表达式为 .
有一段“三段论”推理是这样的:对于可导函数 ,如果
,如果 ,那么
,那么 是
是
函数 的极值点,因为函数
的极值点,因为函数 在
在 处的导数值
处的导数值 ,所以,
,所以, 是函数
是函数 的极值点.以上推理中( )
的极值点.以上推理中( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
已知 不等式
不等式 的解集为
的解集为 ,
, 是减函数,则
是减函数,则 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |