广东省“十二校”高三第2次联考理科数学试卷
已知全集U=R,集合 ,
, ,则A∩(∁UB)=( )
,则A∩(∁UB)=( )
A.(0,1) B. C.(1, 2) D. (0,2)
C.(1, 2) D. (0,2)
已知x,y∈R,i为虚数单位,且(x﹣2)i﹣y=1,则 的值为( )
的值为( )
| A.4 | B.﹣4 | C.﹣2i | D.﹣2+2i |
定义在R上的偶函数f(x)在(0,+∞)上是增函数,且f( )=0,则不等式
)=0,则不等式 的解集是( )
的解集是( )
A.(0, ) ) |
B.( ,+∞) ,+∞) |
C.(- ,0)∪( ,0)∪( ,+∞) ,+∞) |
D.(-∞,- )∪(0, )∪(0, ) ) |
已知双曲线 (
( ,
, ),过其右焦点且垂直于实轴的直线与双曲线交于
),过其右焦点且垂直于实轴的直线与双曲线交于 两点,
两点, 为坐标原点,若
为坐标原点,若 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. |
B. |
C. |
D. |
已知集合M={ },若对于任意
},若对于任意 ,存在
,存在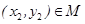 ,使得
,使得 成立,则称集合M是“垂直对点集”.给出下列四个集合:
成立,则称集合M是“垂直对点集”.给出下列四个集合:
①M={ }; ②M={
}; ②M={ };
};
③M={ }; ④M={
}; ④M={ }.
}.
其中是“垂直对点集”的序号是( )
| A.①② | B.②④ | C.①④ | D.②③ |
下面茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损.则甲的平均成绩超过乙的平均成绩的概率为 
下列说法:①“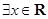 ,
,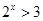 ”的否定是“
”的否定是“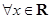 ,
,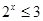 ”;②函数
”;②函数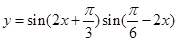 的最小正周期是
的最小正周期是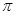 ;③命题“函数
;③命题“函数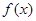 在
在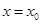 处有极值,则
处有极值,则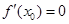 ”的否命题是真命题;④
”的否命题是真命题;④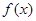 是
是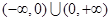 上的奇函数,
上的奇函数,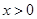 的解析式是
的解析式是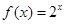 ,则
,则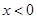 时的解析式为
时的解析式为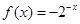 .其中正确的说法是__________.
.其中正确的说法是__________.
已知向量a=(2,1),b=(x,y).若x∈[-1,2],y∈[-1,1],则向量a,b的夹角是钝角的概率是 .
右表给出一个“三角形数阵”.已知每一列数成等差数列,从第三行起,每一行数成等比数列,而且每一行的公比都相等,记第 行第
行第 列的数为
列的数为 (
( ),则
),则 等于 ,
等于 , .
.
在极坐标系中,过点 且垂直于极轴的直线方程的极坐标方程是 (请选择正确标号填空) (1)
且垂直于极轴的直线方程的极坐标方程是 (请选择正确标号填空) (1) (2)
(2)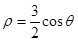 (3)
(3) (4)
(4)
如图,在△ABC和△ACD中,∠ACB=∠ADC=90°,∠BAC=∠CAD,⊙O是以AB为直径的圆,DC的延长线与AB的延长线交于点E. 若EB=6,EC=6,则BC的长为 .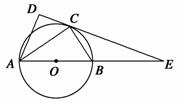
已知函数 (
( )的最小正周期为
)的最小正周期为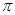 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)将函数 的图象向左平移
的图象向左平移 个单位,再向上平移
个单位,再向上平移 个单位,得到函数
个单位,得到函数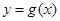 的图象.若
的图象.若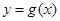 在
在 上至少含有
上至少含有 个零点,求
个零点,求 的最小值.
的最小值.
某高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座。(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各学科讲座各天的满座的概率如下表:
根据上表:
(1)求数学辅导讲座在周一、周三、周五都不满座的概率;
(2)设周三各辅导讲座满座的科目数为 ,求随机变量
,求随机变量 的分布列和数学期望。
的分布列和数学期望。
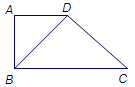
在直角梯形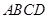 中,
中, ,
,
 ,
, ,如图,把
,如图,把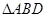 沿
沿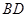 翻折,使得平面
翻折,使得平面 平面
平面 .
.


(1)求证: ;
;
(2)若点 为线段
为线段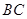 中点,求点
中点,求点 到平面
到平面 的距离;
的距离;
(3)在线段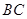 上是否存在点
上是否存在点 ,使得
,使得 与平面
与平面 所成角为
所成角为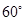 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
设椭圆
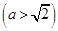 的右焦点为
的右焦点为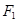 ,直线
,直线 与
与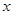 轴交于点
轴交于点 ,若
,若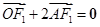 (其中
(其中 为坐标原点).
为坐标原点).
(1)求椭圆 的方程;
的方程;
(2)设 是椭圆
是椭圆 上的任意一点,
上的任意一点,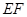 为圆
为圆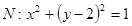 的任意一条直径(
的任意一条直径( 、
、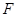 为直径的两个端点),求
为直径的两个端点),求 的最大值.
的最大值.
已知各项均为正数的数列 满足
满足 , 且
, 且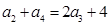 ,其中
,其中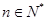 .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 设数列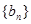 满足
满足 ,是否存在正整数
,是否存在正整数 ,使得
,使得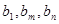 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(3) 令 ,记数列
,记数列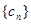 的前
的前 项和为
项和为 ,其中
,其中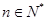 ,证明:
,证明: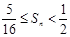 。
。
 ,
, ,则
,则 的值等于( )
的值等于( )



 中,
中, ,前3项和为
,前3项和为 ,则公q的值是( )
,则公q的值是( )
 的展开式的各项系数之和为
的展开式的各项系数之和为 ,二项式系数之和为
,二项式系数之和为 ,若
,若 ,则展开式中的常数项_________.
,则展开式中的常数项_________. ,
, ,
, 图象与
图象与 轴异于原点的交点M处的切线为
轴异于原点的交点M处的切线为 ,
, 与
与 , 并且
, 并且 的值;
的值; 的取值范围及函数
的取值范围及函数 的最小值;
的最小值; ,给定
,给定 ,对于两个大于1的正数
,对于两个大于1的正数 ,存在实数
,存在实数 满足:
满足: ,
, ,并且使得不等式
,并且使得不等式 恒成立,求实数
恒成立,求实数 粤公网安备 44130202000953号
粤公网安备 44130202000953号