有一段“三段论”推理是这样的:对于可导函数 ,如果
,如果 ,那么
,那么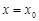 是
是
函数 的极值点,因为函数
的极值点,因为函数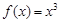 在
在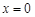 处的导数值
处的导数值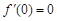 ,所以,
,所以,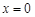 是函数
是函数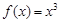 的极值点.以上推理中( )
的极值点.以上推理中( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
相关知识点
推荐套卷
有一段“三段论”推理是这样的:对于可导函数 ,如果
,如果 ,那么
,那么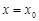 是
是
函数 的极值点,因为函数
的极值点,因为函数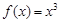 在
在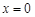 处的导数值
处的导数值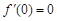 ,所以,
,所以,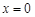 是函数
是函数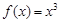 的极值点.以上推理中( )
的极值点.以上推理中( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |