[四川]2011-2012学年四川省泸州高级教育培训学校高三12月月考理科数学
在复平面内,复数 对应的点位于( )
对应的点位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
已知 不等式
不等式 的解集为
的解集为 ,
, 是减函数,则
是减函数,则 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
从圆 外一点
外一点 向这个圆作两条切线,则两切线夹角的余弦值为( )
向这个圆作两条切线,则两切线夹角的余弦值为( )
A. |
B. |
C. |
D. |
已知双曲线 的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
| A.( 1,2) | B.(1,2) | C.[2,+∞] | D.(2,+∞) |
要得到函数 的图象,只需将函数
的图象,只需将函数 的图象作下列移动得到( )
的图象作下列移动得到( )
A.按向量 平移 平移 |
B.按向量 平移 平移 |
C.按向量 平移 平移 |
D.按向量 平移 平移 |
在三角形中,向量 和
和 满足
满足 且
且 则△ABC为( )
则△ABC为( )
| A.等边三角形 | B.等腰非直角三角形 | C.非等腰三角形 | D.等腰直角三角形 |
3位男生和3位女生共6位同学站成一排,若男生甲不站两端,3位女生中有且只有两位女生相邻,则不同排法的种数是( )
| A.360 | B.288 | C.216 | D.228 |
已知R上的连续函数 满足:①当
满足:①当 时,
时, 恒成立(
恒成立( 为函数
为函数 的导函数);②对任意
的导函数);②对任意 都有
都有 。又函数
。又函数 满足:对任意的
满足:对任意的 都有
都有 成立,当
成立,当 时,
时, 。若关于x的不等式
。若关于x的不等式 对
对 恒成立,则a的取值范围是( )
恒成立,则a的取值范围是( )
A. 或 或 |
B. |
C. ? ? |
D. |
已知 的展开式中所有项的二项式系数和为64,则展开式的常数项是_________.
的展开式中所有项的二项式系数和为64,则展开式的常数项是_________.
设过点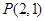 的直线
的直线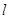 分别与
分别与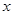 正半轴,
正半轴, 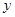 轴正半轴交于
轴正半轴交于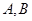 两点,
两点,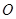 为坐标原点,则三角形
为坐标原点,则三角形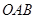 面积最小时直线方程为
面积最小时直线方程为
若定义在R上的函数 满足
满足 ,
, ,则称
,则称 为R上的线性变换,现有下列命题:
为R上的线性变换,现有下列命题:
① 是R上的线性变换
是R上的线性变换
②若 是R上的线性变换,则
是R上的线性变换,则

③若 与
与 均为R上的线性变换,则
均为R上的线性变换,则 是R上的线性变换
是R上的线性变换
④ 是R上的线性变换的充要条件为
是R上的线性变换的充要条件为 是R上的一次函数
是R上的一次函数
其中是真命题有 (写出所有真命题的编号)
在 中,已知内角
中,已知内角 所对的边分别为
所对的边分别为 ,向量
,向量 
 ,且
,且 //
// ,
,  为锐角.
为锐角.
(1)求角 的大小; (2)设
的大小; (2)设 ,求
,求 的面积
的面积 的最大值.
的最大值.
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(Ⅰ)求在1次游戏中,(i)摸出3个白球的概率;(ii)获奖的概率;
(Ⅱ)求在2次游戏中获奖次数 的分布列及数学期望
的分布列及数学期望 .
.
圆C与y轴相切,圆心在射线 x-3y=0(x>0)上,且圆C截直线y=x所得弦长为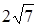 . (1)求圆C的方程。(2)点P(x,y)是圆C上的动点,求x+y的最大值。(3)求过点M(2,1)的圆的弦的中点轨迹方程。
. (1)求圆C的方程。(2)点P(x,y)是圆C上的动点,求x+y的最大值。(3)求过点M(2,1)的圆的弦的中点轨迹方程。
已知数列 的前n项和为
的前n项和为 ,且满足
,且满足
(1)求数列 的通项公式;
的通项公式;
(2)若 的前n项和为
的前n项和为 求满足不等式
求满足不等式 的最小n值.
的最小n值.
已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,两准线间的距离为4.
(Ⅰ)求椭圆的方程;
(Ⅱ)直线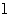 过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程.
过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程.
 =( )
=( )



 ,则
,则 在
在 方向上的投影为( )
方向上的投影为( )



 在x=2处连续,则常数
在x=2处连续,则常数 的值是( )
的值是( ) 满足条件
满足条件 那么
那么 的最大值为( )
的最大值为( )



 的首项
的首项 ,其前
,其前 项的和为
项的和为 ,且
,且 ,则
,则 ____
____  满足:
满足: 记y=f(x).
记y=f(x).  不等式|a-lnx|-ln[f'(x)-3x]>0恒成立,求实数a的取值范围:
不等式|a-lnx|-ln[f'(x)-3x]>0恒成立,求实数a的取值范围: 粤公网安备 44130202000953号
粤公网安备 44130202000953号