学校游园活动有这样一个游戏项目：甲箱子里装有3个白球、2个黑球，乙箱子里装有1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖．（每次游戏结束后将球放回原箱）
（Ⅰ）求在1次游戏中，（i）摸出3个白球的概率；（ii）获奖的概率；
（Ⅱ）求在2次游戏中获奖次数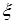
的分布列及数学期望
.
相关试题
、
、
，动点
满足：
、
时，求
的最大值和最小值、
其中x∈[0，
]、
的最大值和最小值；
⊥
，求|
|、
的夹角
的余弦用x表示的函数
；
、推荐套卷
学校游园活动有这样一个游戏项目：甲箱子里装有3个白球、2个黑球，乙箱子里装有1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖．（每次游戏结束后将球放回原箱）
（Ⅰ）求在1次游戏中，（i）摸出3个白球的概率；（ii）获奖的概率；
（Ⅱ）求在2次游戏中获奖次数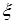的分布列及数学期望 .
粤公网安备 44130202000953号