高中数学组合几何解答题

(本小题满分12分)函数，．
（Ⅰ）求的单调区间和最小值；
（Ⅱ）讨论与的大小关系；
（Ⅲ）是否存在，使得对任意成立？若存在，求出的取值范围；若不存在，请说明理由．

画出的图象，求出其在点处的切线方程，并画出切线．

已知函数 (＞0)的图象在点处的切线方程为.
(1)用表示；
(2)若在上恒成立，求的取值范围；
(3)证明：1+++…+＞+.

路灯距地平面为,一个身高为的人以的速率在地面上行走，从路灯在地平面上射影点C，沿某直线离开路灯，求人影长度的变化速率v.

用三段论证明函数在（－∞，+∞）上是增函数.

比较函数与,当时,平均增长率的大小.

已知函数，过点作曲线的切线，求切线方程．

已知曲线与在处的切线互相垂直，求的值 

（本小题满分10分）(1)求函数的导数.
(2)求函数f(x)=在区间［0，3］上的积分.

(6分)（1） 求三次曲线过点(2, 8)的切线方程；
（2）求曲线过点（0，0）的切线方程。

已知曲线与在处的切线互相垂直,求的值.

曲线在点处的切线与x轴交点的横坐标为a_n．
（1）求a_n；
（2）设，求数到的前n项和S_n．

已知函数．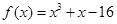
（1）求曲线在点处的切线方程；
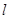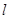（2）直线为曲线的切线，且经过原点，求直线的方程及切点坐标．

已知函数f(x)=x－ax+(a－1)，。
（1）讨论函数的单调性；       
（2）证明：若，则对任意x，x，xx，有。

(本小题满分l2分)求垂直于直线并且与曲线相切的直线方程.