已知函数 与
与 轴相切
轴相切 若直线
若直线 与
与 分别交
分别交 的图象于
的图象于 四点
四点 且四边形
且四边形 的面积为25
的面积为25 则正实数
则正实数 的值为
的值为
已知函数f(x)=x(x+a)-lnx,其中a为常数.
(1)求f(x)的单调区间;
(2)问过坐标原点可以作几条直线与曲线y=f(x)相切?并说明理由;
(3)若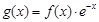 在区间(0,1)内是单调函数,求a的取值范围.
在区间(0,1)内是单调函数,求a的取值范围.
已知函数 (k为常数,e=2.71828…是自然对数的底数),曲线
(k为常数,e=2.71828…是自然对数的底数),曲线 在点
在点 处的切线与x轴平行.
处的切线与x轴平行.
(1)求k的值及 的单调区间;
的单调区间;
(2)设 其中
其中 为
为 的导函数,证明:对任意
的导函数,证明:对任意 ,
, .
.
已知 的图像过原点,且在点
的图像过原点,且在点 处的切线与
处的切线与 轴平行,对任意
轴平行,对任意 ,都有
,都有 .
.
(1)求函数 在点
在点 处切线的斜率;
处切线的斜率;
(2)求 的解析式;
的解析式;
(3)设 ,对任意
,对任意 ,都有
,都有 .求实数
.求实数 的取值范围.
的取值范围.
已知函数 的图象与直线
的图象与直线 交于点P,若图象在点P处的切线与x轴交点的横坐标为
交于点P,若图象在点P处的切线与x轴交点的横坐标为 ,则
,则 +
+ +…+
+…+ 的值为( )
的值为( )
| A.-1 | B.1-log20132012 | C.-log20132012 | D.1 |
已知函数 (
( 为常数).
为常数).
(1)若 是函数
是函数 的一个极值点,求
的一个极值点,求 的值;
的值;
(2)当 时,试判断
时,试判断 的单调性;
的单调性;
(3)若对任意的
 ,使不等式
,使不等式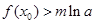 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知函数 .
.
(1)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若函数 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围;
(3)设函数 ,若在
,若在 上至少存在一点
上至少存在一点 ,使得
,使得 >
> 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知函数f(x)=ax2+1,g(x)=x3+bx,其中a>0,b>0.
(1)若曲线y=f(x)与曲线y=g(x) 在它们的交点P(2,c)处有相同的切线(P为切点),求实数a,b的值;
(2)令h (x)=f(x)+g(x),若函数h(x)的单调减区间为 .
.
①求函数h(x)在区间(-∞,-1]上的最大值M(a);
②若|h(x)|≤3在x∈[-2,0]上恒成立,求实数a的取值范围.
已知函数f(x)=ax+x2-xln a(a>0,a≠1).
(1)求函数f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)的单调增区间;
(3)若存在x1,x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1(e是自然对数的底数),求实数a的取值范围.