已知定义在R上的函数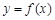 满足条件
满足条件 ,且函数
,且函数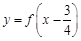
是奇函数,给出以下四个命题:
①函数 是周期函数;②函数
是周期函数;②函数 的图象关于点
的图象关于点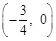 对称;
对称;
③函数 是偶函数;④函数
是偶函数;④函数 在R上是单调函数.
在R上是单调函数.
在上述四个命题中,正确命题的序号是__________(写出所有正确命题的序号).
已知定义域为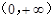 的函数
的函数 满足:①对任意
满足:①对任意 ,恒有
,恒有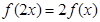 成立;当
成立;当 时,
时,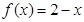 。给出如下结论:
。给出如下结论:
①对任意 ,有
,有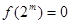 ;②函数
;②函数 的值域为
的值域为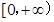 ;③存在
;③存在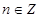 ,使得
,使得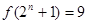 ;④“函数
;④“函数 在区间
在区间 上单调递减”的充要条件是 “存在
上单调递减”的充要条件是 “存在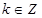 ,使得
,使得 ”。其中所有正确结论的序号是 。
”。其中所有正确结论的序号是 。
下列命题:
①函数 在
在 上是减函数;
上是减函数;
②点A(1,1)、B(2,7)在直线 两侧;
两侧;
③数列 为递减的等差数列,
为递减的等差数列, ,设数列
,设数列 的前n项和为
的前n项和为 ,则当
,则当 时,
时, 取得最大值;
取得最大值;
④定义运算
 则函数
则函数
 的图象在点
的图象在点 处的切线方程是
处的切线方程是 其中正确命题的序号是 (把所有正确命题的序号都写上).
其中正确命题的序号是 (把所有正确命题的序号都写上).
下列命题中_________为真命题.
①“A∩B=A”成立的必要条件是“A B”; w ②“若x2+y2=0,则x,y全为0”的否命题;
B”; w ②“若x2+y2=0,则x,y全为0”的否命题;
③“全等三角形是相似三角形”的逆命题; ④“圆内接四边形对角互补”的逆否命题.
设函数 的定义域为
的定义域为 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 为
为 上的“
上的“ 高调函数”.现给出下列命题:
高调函数”.现给出下列命题:
①函数 为
为 上的“1高调函数”;
上的“1高调函数”;
②函数 为
为 上的“
上的“ 高调函数”;
高调函数”;
③如果定义域为 的函数
的函数 为
为 上“
上“ 高调函数”,那么实数
高调函数”,那么实数 的取值范围是
的取值范围是 ;
;
其中正确的命题是 .(写出所有正确命题的序号)
记 为不超过实数
为不超过实数 的最大整数,例如,
的最大整数,例如, ,
, ,
, 。设
。设 为正整数,数列
为正整数,数列 满足
满足 ,
, ,现有下列命题:
,现有下列命题:
①当 时,数列
时,数列 的前3项依次为5,3,2;
的前3项依次为5,3,2;
②对数列 都存在正整数
都存在正整数 ,当
,当 时总有
时总有 ;
;
③当 时,
时, ;
;
④对某个正整数 ,若
,若 ,则
,则 。
。
其中的真命题有____________。(写出所有真命题的编号
给出下列命题:
①  是
是 的既不充分也不必要的条件;
的既不充分也不必要的条件;
②“p为真”是“p且q为真”的必要不充分条件;
③数列 为等比数列是数列
为等比数列是数列  为等比数列的充分不必要条件;
为等比数列的充分不必要条件;
④a=2是f(x)=|x-a|在[2 ,+∞)上为增函数的充要条件。其中真命题的序号是________.
.给出以下五个命题:①  ,若
,若 ,则x = 0或y = 0的否命题是假命题; ②函数
,则x = 0或y = 0的否命题是假命题; ②函数 的最小值为2; ③若函数
的最小值为2; ③若函数 的图象关于点(1,0)对称,则a的值为-3; ④若
的图象关于点(1,0)对称,则a的值为-3; ④若 ,则函数
,则函数 是以4为周期的周期函数;⑤若
是以4为周期的周期函数;⑤若 ,则
,则 其中真命题的序号是 ________
其中真命题的序号是 ________