已知函数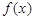 的定义域为
的定义域为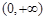 ,若
,若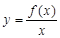 在
在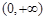 上为增函数,则称
上为增函数,则称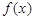 为“一阶比增函数”;若
为“一阶比增函数”;若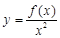 在
在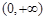 上为增函数,则称
上为增函数,则称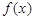 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为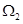 .
.
(Ⅰ)已知函数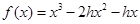 ,若
,若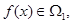 且
且 ,求实数
,求实数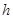 的取值范围;
的取值范围;
(Ⅱ)已知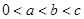 ,
,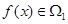 且
且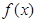 的部分函数值由下表给出,
的部分函数值由下表给出,
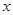 |
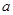 |
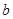 |
 |
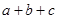 |
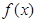 |
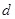 |
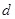 |
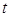 |
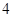 |
求证: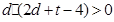 ;
;
(Ⅲ)定义集合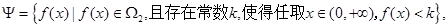
请问:是否存在常数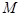 ,使得
,使得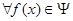 ,
,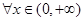 ,有
,有 成立?若存在,求出
成立?若存在,求出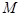 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
已知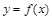 是定义在R上周期为4的奇函数,且
是定义在R上周期为4的奇函数,且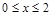 时,
时, 则
则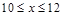 时,
时,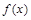 =_________________
=_________________
设函数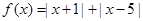 ,
,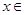
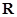 .
.
⑴ 求不等式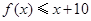 的解集;
的解集;
⑵ 如果关于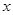 的不等式
的不等式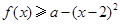 在
在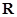 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
已知函数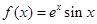 .
.
⑴ 求函数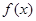 的单调区间;
的单调区间;
⑵ 如果对于任意的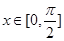 ,
,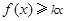 总成立,求实数
总成立,求实数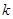 的取值范围;
的取值范围;
⑶ 设函数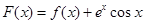 ,
,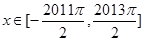 . 过点
. 过点 作函数
作函数 图像的所有切线,令各切点的横坐标构成数列
图像的所有切线,令各切点的横坐标构成数列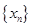 ,求数列
,求数列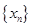 的所有项之和
的所有项之和 的值.
的值.
已知两条直线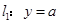 和
和 (其中
(其中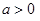 ),
), 与函数
与函数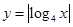 的图像从左至右相交于点
的图像从左至右相交于点 ,
, ,
, 与函数
与函数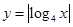 的图像从左至右相交于点
的图像从左至右相交于点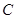 ,
,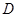 .记线段
.记线段 和
和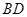 在
在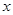 轴上的投影长度分别为
轴上的投影长度分别为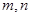 .当
.当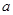 变化时,
变化时,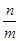 的最小值为( )
的最小值为( )
A.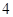 |
B.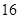 |
C.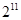 |
D.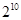 |
对于函数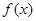 与
与 和区间D,如果存在
和区间D,如果存在 ,使
,使 ,则称
,则称 是函数
是函数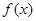 与
与 在区间D上的“友好点”.现给出两个函数:
在区间D上的“友好点”.现给出两个函数:
① ,
, ;
;
② ,
,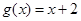 ;
;
③ ,
,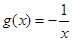 ;
;
④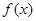
 ,
, ,
,
则在区间 上的存在唯一“友好点”的是( )
上的存在唯一“友好点”的是( )
| A.①② | B.③④ | C.②③ | D.①④ |
已知函数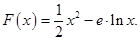
(I)求函数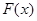 的最小值;
的最小值;
(II)对于函数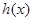 和
和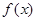 定义域内的任意实数
定义域内的任意实数 ,若存在常数
,若存在常数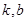 ,使得不等式
,使得不等式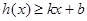 和
和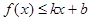 都成立,则称直线
都成立,则称直线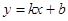 是函数
是函数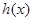 和
和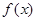 的“分界线”.
的“分界线”.
设函数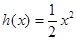 ,
,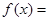
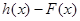 ,试问函数
,试问函数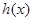 和
和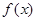 是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
已知函数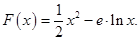
(I)求函数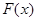 的极值;
的极值;
(II)对于函数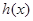 和
和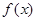 定义域内的任意实数
定义域内的任意实数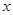 ,若存在常数
,若存在常数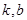 ,使得不等式
,使得不等式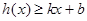 和
和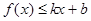 都成立,则称直线
都成立,则称直线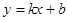 是函数
是函数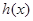 和
和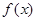 的“分界线”.
的“分界线”.
设函数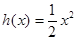 ,
,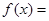
 ,试问函数
,试问函数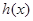 和
和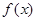 是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
已知函数 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是 ,则不等式组
,则不等式组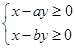 所确定的平面区域在
所确定的平面区域在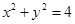 内的面积为 ( )
内的面积为 ( )
A. |
B.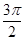 |
C.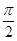 |
D.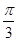 |
已知函数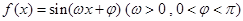 在一个周期内的部分对应值如下表:
在一个周期内的部分对应值如下表:
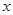 |
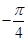 |
 |
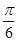 |
 |
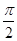 |
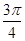 |
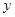 |
 |
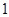 |
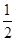 |
 |
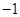 |
 |
(I)求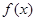 的解析式;
的解析式;
(II)设函数 ,
,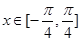 ,求
,求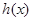 的最大值和最小值.
的最大值和最小值.
已知函数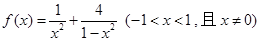 .
.
(Ⅰ)求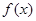 的最小值;
的最小值;
(Ⅱ)若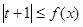 恒成立,求实数
恒成立,求实数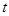 的取值范围.
的取值范围.