[吉林]2013届吉林省吉林市高三三模(期末)理科数学试卷
某几何体的三视图如图所示,其正视图,侧视图,俯视图均为全等的正方形,则该几何体的体积为( )
A. |
B. |
C.  |
D. |
为了得到函数 的图象,可以将函数
的图象,可以将函数 的图象( )
的图象( )
A.向右平移 个单位长度 个单位长度 |
B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 |
D.向左平移 个单位长度 个单位长度 |
中心为 , 一个焦点为
, 一个焦点为 的椭圆,截直线
的椭圆,截直线 所得弦中点的横坐标为
所得弦中点的横坐标为 ,则该椭圆方程是( )
,则该椭圆方程是( )
A. |
B. |
C. |
D. |
下列说法错误的是( )
A. 是 是 或 或 的充分不必要条件 的充分不必要条件 |
B.若命题  ,则 ,则  |
C.已知随机变量 ,且 ,且 ,则 ,则 |
D.相关指数 越接近 越接近 ,表示残差平方和越大. ,表示残差平方和越大. |
已知 ,并设:
,并设:
 ,
, 至少有3个实根;
至少有3个实根; 当
当 时,方程
时,方程 有9个实根;
有9个实根; 当
当 时,方程
时,方程 有5个实根。
有5个实根。
则下列命题为真命题的是( )
A. |
B. |
C.仅有 |
D. |
设圆 和圆
和圆 是两个定圆,动圆P与这两个定圆都相切,则圆P的圆心轨迹可能是( )
是两个定圆,动圆P与这两个定圆都相切,则圆P的圆心轨迹可能是( )




① ② ③ ④ ⑤
| A.①③⑤ | B.②④⑤ | C.①②④ | D.①②③ |
在一次考试中,5名学生的数学和物理成绩如下表:(已知学生的数学和物理成绩具有线性相关关系)
| 学生的编号i |
1 |
2 |
3 |
4 |
5 |
| 数学成绩x |
80 |
75 |
70 |
65 |
60 |
| 物理成绩y |
70 |
66 |
68 |
64 |
62 |
现已知其线性回归方程为 ,则根据此线性回归方程估计数学得90分的同学的物理成绩为 .(四舍五入到整数)
,则根据此线性回归方程估计数学得90分的同学的物理成绩为 .(四舍五入到整数)
下列命题中正确的是 .(填上你认为所有正确的选项)
①空间中三个平面 ,若
,若 ,则
,则 ∥
∥ ;
;
②若 为三条两两异面的直线,则存在无数条直线与
为三条两两异面的直线,则存在无数条直线与 都相交;
都相交;
③球 与棱长为
与棱长为 正四面体各面都相切,则该球的表面积为
正四面体各面都相切,则该球的表面积为 ;
;
④三棱锥 中,
中, 则
则 .
.
设等比数列{ }的前
}的前 项和为
项和为 ,已知对任意的
,已知对任意的 ,点
,点 ,均在函数
,均在函数 的图像上.
的图像上.
(Ⅰ)求 的值;
的值;
(Ⅱ)记 求数列
求数列 的前
的前 项和
项和 .
.
某班同学在“十八大”期间进行社会实践活动,对[25,55]岁的人群随机抽取 人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:
人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:
(Ⅰ)求n,a,p的值;
(Ⅱ)从年龄在[40,50)岁的“房地产投资”人群中采取分层抽样法抽取9人参加投资管理学习活动,其中选取3人作为代表发言,记选取的3名代表中年龄在[40,45)岁的人数为 ,求
,求 的分布列和期望
的分布列和期望 .
.

如图,在四棱锥 中,
中, ⊥底面
⊥底面 ,四边形
,四边形 是直角梯形,
是直角梯形, ⊥
⊥ ,
, ∥
∥ ,
, .
.

(Ⅰ)求证:平面 ⊥平面
⊥平面 ;
;
(Ⅱ)若二面角 的余弦值为
的余弦值为 ,求
,求 .
.
设 为抛物线
为抛物线 (
( )的焦点,
)的焦点, 为该抛物线上三点,若
为该抛物线上三点,若 ,且
,且
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ) 点的坐标为(
点的坐标为( ,
, )其中
)其中 ,过点F作斜率为
,过点F作斜率为 的直线与抛物线交于
的直线与抛物线交于 、
、 两点,
两点, 、
、 两点的横坐标均不为
两点的横坐标均不为 ,连结
,连结 、
、 并延长交抛物线于
并延长交抛物线于 、
、 两点,设直线
两点,设直线 的斜率为
的斜率为 .若
.若 ,求
,求 的值.
的值.
如图,设AB,CD为⊙O的两直径,过B作PB垂直于AB,并与CD延长线相交于点P,过P作直线与⊙O分别交于E,F两点,连结AE,AF分别与CD交于G、H
(Ⅰ)设EF中点为 ,求证:O、
,求证:O、 、B、P四点共圆
、B、P四点共圆
(Ⅱ)求证:OG =OH.
极坐标系中椭圆C的方程为 以极点为原点,极轴为
以极点为原点,极轴为 轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
(Ⅰ)求该椭圆的直角标方程;若椭圆上任一点坐标为 ,求
,求 的取值范围;
的取值范围;
(Ⅱ)若椭圆的两条弦 交于点
交于点 ,且直线
,且直线 与
与 的倾斜角互补,
的倾斜角互补,
求证: .
.
 ( )
( )



 ②
② ③
③ ④
④ ,其中是奇函数的是( )
,其中是奇函数的是( ) ,集合
,集合 ,则
,则 ( )
( )



 在不等式组
在不等式组 表示的平面区域上运动,则
表示的平面区域上运动,则 的取值范围是( )
的取值范围是( )



 的值是( )
的值是( )
 始终平分圆
始终平分圆 的周长,则
的周长,则 的最小值为( )
的最小值为( )



 的展开式中
的展开式中 的系数为
的系数为 ,则
,则 的值为____________.
的值为____________. 中,角
中,角 所对的边分别为
所对的边分别为 满足
满足 ,
, ,
, ,则
,则 的取值范围是 .
的取值范围是 . 的函数
的函数
 ,在
,在 处的切线斜率为
处的切线斜率为
 及
及 的单调区间;
的单调区间; 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.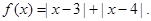
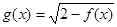 的定义域;
的定义域;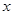 满足
满足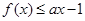 ,试求实数
,试求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号