设 为抛物线
为抛物线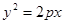 (
(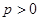 )的焦点,
)的焦点, 为该抛物线上三点,若
为该抛物线上三点,若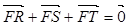 ,且
,且
(Ⅰ)求抛物线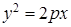 的方程;
的方程;
(Ⅱ)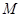 点的坐标为(
点的坐标为(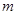 ,
, )其中
)其中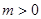 ,过点F作斜率为
,过点F作斜率为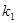 的直线与抛物线交于
的直线与抛物线交于 、
、 两点,
两点, 、
、 两点的横坐标均不为
两点的横坐标均不为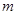 ,连结
,连结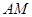 、
、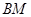 并延长交抛物线于
并延长交抛物线于 、
、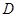 两点,设直线
两点,设直线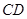 的斜率为
的斜率为 .若
.若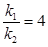 ,求
,求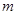 的值.
的值.
推荐套卷
设 为抛物线
为抛物线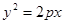 (
(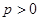 )的焦点,
)的焦点, 为该抛物线上三点,若
为该抛物线上三点,若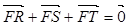 ,且
,且
(Ⅰ)求抛物线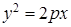 的方程;
的方程;
(Ⅱ)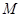 点的坐标为(
点的坐标为(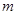 ,
, )其中
)其中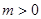 ,过点F作斜率为
,过点F作斜率为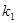 的直线与抛物线交于
的直线与抛物线交于 、
、 两点,
两点, 、
、 两点的横坐标均不为
两点的横坐标均不为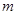 ,连结
,连结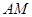 、
、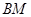 并延长交抛物线于
并延长交抛物线于 、
、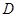 两点,设直线
两点,设直线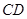 的斜率为
的斜率为 .若
.若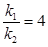 ,求
,求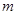 的值.
的值.