极坐标系中椭圆C的方程为
以极点为原点，极轴为
轴非负半轴，建立平面直角坐标系，且两坐标系取相同的单位长度.
（Ⅰ）求该椭圆的直角标方程；若椭圆上任一点坐标为
，求
的取值范围；
（Ⅱ）若椭圆的两条弦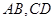
交于点
，且直线
与
的倾斜角互补，
求证:
.
相关试题
后得到的
－5）2+（
+4）2=1，求曲线C的方程，并判断其形状。
，PO=12.求⊙O的半径。
，（t为参数，a∈R）点
推荐套卷
极坐标系中椭圆C的方程为以极点为原点，极轴为轴非负半轴，建立平面直角坐标系，且两坐标系取相同的单位长度.
（Ⅰ）求该椭圆的直角标方程；若椭圆上任一点坐标为，求的取值范围；
（Ⅱ）若椭圆的两条弦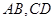交于点，且直线与的倾斜角互补，
求证:.
粤公网安备 44130202000953号