[福建]2013届福建福州市高中毕业班质量检查理科数学试卷
要得到函数 的图象,只须将
的图象,只须将 的图象上的所有的点( )
的图象上的所有的点( )
A.向左平移 个单位长度 个单位长度 |
B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 |
D.向右平移 个单位长度 个单位长度 |
根据某市环境保护局公布2007-2012这六年每年的空气质量优良的天数,绘制折线图如图.根据图中信息可知,这六年的每年空气质量优良天数的中位数是( )
A. |
B. |
C. |
D. |
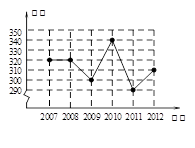
已知函数 ,则“
,则“ ”是“函数
”是“函数 在
在 上为增函数”的( )
上为增函数”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题“直线 与平面
与平面 有公共点”是真命题,那么下列命题:
有公共点”是真命题,那么下列命题:
①直线 上的点都在平面
上的点都在平面 内;
内;
②直线 上有些点不在平面
上有些点不在平面 内;
内;
③平面 内任意一条直线都不与直线
内任意一条直线都不与直线 平行.
平行.
其中真命题的个数是( )
| A.3 | B.2 | C.1 | D.0 |
已知等比数列 的公比
的公比 ,且
,且 成等差数列,则
成等差数列,则 的前8项和为( )
的前8项和为( )
| A.127 | B.255 | C.511 | D.1023 |
已知点 是△
是△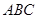 所在平面内的一点,边AB的中点为D,若
所在平面内的一点,边AB的中点为D,若 ,其中
,其中 ,则点
,则点 一定在( )
一定在( )
| A.AB边所在的直线上 | B.BC边所在的直线上 |
| C.AC边所在的直线上 | D.△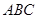 的内部 的内部 |
对于任意给定的实数 ,直线
,直线 与双曲线
与双曲线 ,
, 最多有一个交点,则双曲线的离心率等于( )
最多有一个交点,则双曲线的离心率等于( )
A. |
B.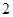 |
C. |
D. |
对于函数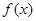 与
与 和区间D,如果存在
和区间D,如果存在 ,使
,使 ,则称
,则称 是函数
是函数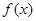 与
与 在区间D上的“友好点”.现给出两个函数:
在区间D上的“友好点”.现给出两个函数:
① ,
, ;
;
② ,
,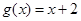 ;
;
③ ,
,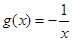 ;
;
④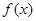
 ,
, ,
,
则在区间 上的存在唯一“友好点”的是( )
上的存在唯一“友好点”的是( )
| A.①② | B.③④ | C.②③ | D.①④ |
已知程序框图如右图所示,执行该程序,如果输入 ,输出
,输出 ,则在图中“?”处可填入的算法语句是 (写出以下所有满足条件的序号).
,则在图中“?”处可填入的算法语句是 (写出以下所有满足条件的序号).
①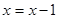 ;
;
② ;
;
③ ;
;
④ .
.
数列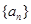 是由集合
是由集合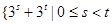 ,且
,且 ,
,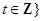 中所有的数从小到大排列成的数列,即
中所有的数从小到大排列成的数列,即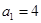 ,
, ,
,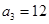 ,
, ,a5=30,a6=36,…,若
,a5=30,a6=36,…,若 =
=
 ,且
,且 ,
, ,则
,则 的值等于____________.
的值等于____________.
已知平面向量a ,b=
,b=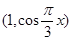 ,定义函数
,定义函数


(Ⅰ)求函数 的值域;
的值域;
(Ⅱ)若函数 图象上的两点
图象上的两点 、
、 的横坐标分别为
的横坐标分别为 和
和 ,
, 为坐标原点,求△
为坐标原点,求△ 的面积.
的面积.
某校高三2班有48名学生进行了一场投篮测试,其中男生28人,女生20人.为了了解其投篮成绩,甲、乙两人分别对全班的学生进行编号(1~48号),并以不同的方法进行数据抽样,其中一人用的是系统抽样,另一人用的是分层抽样.若此次投篮考试的成绩大于或等于80分视为优秀,小于80分视为不优秀,以下是甲、乙两人分别抽取的样本数据:
(Ⅰ)从甲抽取的样本数据中任取两名同学的投篮成绩,记“抽到投篮成绩优秀”的人数为X,求X的分布列和数学期望;
(Ⅱ)请你根据乙抽取的样本数据完成下列2×2列联表,判断是否有95%以上的把握认为投篮成绩和性别有关?
(Ⅲ)判断甲、乙各用何种抽样方法,并根据(Ⅱ)的结论判断哪种抽样方法更优?说明理由.
下面的临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
6.635 |
7.879 |
10.828 |
(参考公式: ,其中
,其中 )
)
如图,已知多面体 的底面
的底面 是边长为
是边长为 的正方形,
的正方形, 底面
底面 ,
,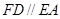 ,且
,且 .
.
(Ⅰ)求多面体 的体积;
的体积;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(Ⅲ)记线段BC的中点为K,在平面ABCD内过点K作一条直线与平面 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
已知
 ,曲线
,曲线 上任意一点
上任意一点 分别与点
分别与点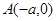 、
、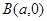 连线的斜率的乘积为
连线的斜率的乘积为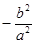 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)设直线 与
与 轴、
轴、 轴分别交于
轴分别交于 、
、 两点,若曲线
两点,若曲线 与直线
与直线 没有公共点,求证:
没有公共点,求证: .
.
已知函数 .
.
(Ⅰ)当 时,求曲线
时,求曲线 在原点处的切线方程;
在原点处的切线方程;
(Ⅱ)当 时,讨论函数
时,讨论函数 在区间
在区间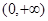 上的单调性;
上的单调性;
(Ⅲ)证明不等式 对任意
对任意 成立.
成立.
已知线性变换 :
: 对应的矩阵为
对应的矩阵为 ,向量β
,向量β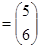 .
.
(Ⅰ)求矩阵 的逆矩阵
的逆矩阵 ;
;
(Ⅱ)若向量α在 作用下变为向量β,求向量α.
作用下变为向量β,求向量α.
在极坐标系中,圆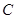 的极坐标方程为
的极坐标方程为 .现以极点
.现以极点 为原点,极轴为
为原点,极轴为 轴的非负半轴建立平面直角坐标系.
轴的非负半轴建立平面直角坐标系.
(Ⅰ)求圆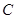 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若圆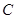 上的动点
上的动点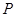 的直角坐标为
的直角坐标为 ,求
,求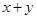 的最大值,并写出
的最大值,并写出 取得最大值时点P的直角坐标.
取得最大值时点P的直角坐标.
 是虚数单位,复数
是虚数单位,复数 ,
, .若
.若 的虚部为
的虚部为 ,则
,则 等于( )
等于( ) 则
则 中奇数的个数为( )
中奇数的个数为( )

 ,则
,则 的值等于 .
的值等于 .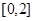 上任取两个数
上任取两个数 ,
,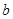 ,能使函数
,能使函数
 在区间
在区间 内有零点的概率等于________.
内有零点的概率等于________. 的解集为
的解集为 .
. 的值;
的值; ,求
,求 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号