[贵州]2013届贵州黔东南州高三第二次模拟(5月)考试理科数学试卷
某中学从 名男生和
名男生和 名女生中推荐
名女生中推荐 人参加社会公益活动,若选出的
人参加社会公益活动,若选出的 人中既有男生又有女生,则不同的选法共有( )
人中既有男生又有女生,则不同的选法共有( )
A. 种 种 |
B. 种 种 |
C. 种 种 |
D. 种 种 |
某市进行一次高三数学质量抽样检测,考试后统计发现考生的数学成绩服从正态分布 ,其中
,其中 分以下的考生人数占
分以下的考生人数占 ,则数学成绩在
,则数学成绩在 至
至 分之间的考生人数所占百分比约为 ( )
分之间的考生人数所占百分比约为 ( )
A. |
B. |
C. |
D. |
已知函数 ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )
A.函数 的图象关于直线 的图象关于直线 对称 对称 |
B.函数 的最大值为 的最大值为 |
C.函数 在区间 在区间 上是增函数 上是增函数 |
D.函数 的最小正周期为 的最小正周期为 |
阅读图 的程序框图,若输出的
的程序框图,若输出的 的值等于
的值等于 ,那么在程序框图中判断框内应填写的条件是( )
,那么在程序框图中判断框内应填写的条件是( )
A. ? ? |
B. ? ? |
C. ? ? |
D. ? ? |

如图 ,在透明塑料制成的长方体
,在透明塑料制成的长方体 容器内灌进一些水,将容器底面一边
容器内灌进一些水,将容器底面一边 固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
①水的部分始终呈棱柱状;
②水面四边形 的面积不改变;
的面积不改变;
③棱 始终与水面
始终与水面 平行;
平行;
④当 时,
时, 是定值.
是定值.
其中所有正确的命题的序号是 ( )
| A.①②③ | B.①③ | C.②④ | D.①③④ |

已知抛物线 的焦点
的焦点 恰为双曲线
恰为双曲线 的右焦点,且两曲线交点的连线过点
的右焦点,且两曲线交点的连线过点 ,则双曲线的离心率为 ( )
,则双曲线的离心率为 ( )
A. |
B. |
C. |
D. |
已知函数 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是 ,则不等式组
,则不等式组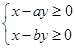 所确定的平面区域在
所确定的平面区域在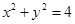 内的面积为 ( )
内的面积为 ( )
A. |
B.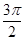 |
C.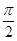 |
D.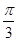 |
已知定义在 上的函数
上的函数 是周期为
是周期为 的偶函数,当
的偶函数,当 时,
时, ,如果直线
,如果直线 与曲线
与曲线 恰有两个交点,则实数
恰有两个交点,则实数 的值是( )
的值是( )
A. |
B. |
C. 或 或 |
D. 或 或 |
设数列 满足:
满足: 点
点 均在直线
均在直线 上.
上.
(I)证明数列 为等比数列,并求出数列
为等比数列,并求出数列 的通项公式;
的通项公式;
(II)若 ,求数列
,求数列 的前
的前 项和
项和 .
.
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
频率分布表
| 组别 |
分组 |
频数 |
频率 |
| 第1组 |
[50,60) |
8 |
0.16 |
| 第2组 |
[60,70) |
a |
▓ |
| 第3组 |
[70,80) |
20 |
0.40 |
| 第4组 |
[80,90) |
▓ |
0.08 |
| 第5组 |
[90,100] |
2 |
b |
| |
合计 |
▓ |
▓ |
频率分布直方图
、
(Ⅰ)写出 的值;
的值;
(Ⅱ)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动,设 表示所抽取的2名同学中来自第5组的人数,求
表示所抽取的2名同学中来自第5组的人数,求 的分布列及其数学期望.
的分布列及其数学期望.
如图,在直三棱柱(即侧棱与底面垂直的三棱柱) 中,
中,

(I)若 为
为 的中点,求证:平面
的中点,求证:平面 平面
平面 ;
;
(II)若 为线段
为线段 上一点,且二面角
上一点,且二面角 的大小为
的大小为 ,试确定
,试确定 的位置.
的位置.
已知动点 与定点
与定点 的距离和它到直线
的距离和它到直线 的距离之比是常数
的距离之比是常数 ,记
,记 的轨迹为曲线
的轨迹为曲线 .
.
(I)求曲线 的方程;
的方程;
(II)设直线 与曲线
与曲线 交于
交于 两点,点
两点,点 关于
关于 轴的对称点为
轴的对称点为 ,试问:当
,试问:当 变化时,直线
变化时,直线 与
与 轴是否交于一个定点?若是,请写出定点的坐标,并证明你的结论;若不是,请说明理由.
轴是否交于一个定点?若是,请写出定点的坐标,并证明你的结论;若不是,请说明理由.
已知函数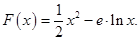
(I)求函数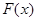 的极值;
的极值;
(II)对于函数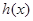 和
和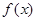 定义域内的任意实数
定义域内的任意实数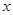 ,若存在常数
,若存在常数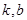 ,使得不等式
,使得不等式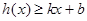 和
和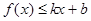 都成立,则称直线
都成立,则称直线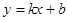 是函数
是函数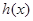 和
和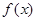 的“分界线”.
的“分界线”.
设函数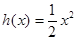 ,
,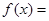
 ,试问函数
,试问函数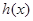 和
和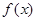 是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
已知在直角坐标系 中,曲线
中,曲线 的参数方程为:
的参数方程为: (
( 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线 的极坐标方程为:
的极坐标方程为: .
.
(Ⅰ)写出曲线 和直线
和直线 在直角坐标系下的方程;
在直角坐标系下的方程;
(II)设点 是曲线
是曲线 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值.
 是虚数单位,若复数
是虚数单位,若复数 是纯虚数,则实数
是纯虚数,则实数 等于 ( )
等于 ( )



 ,且
,且 ,则集合
,则集合 可能是( )
可能是( )



 ,且
,且 ,则
,则 的值等于( )
的值等于( )


 ,根据函数的性质、积分的性质和积分的几何意义计算
,根据函数的性质、积分的性质和积分的几何意义计算 的值为( )
的值为( )



 的展开式中,常数项为_________. (用数字作答)
的展开式中,常数项为_________. (用数字作答) 及其三视图中的主视图和左视图如图所示,则棱
及其三视图中的主视图和左视图如图所示,则棱 的长为_________.
的长为_________.
 在球心为
在球心为 的球面上,
的球面上, 的内角
的内角 ,且
,且 ,球心
,球心 的距离为
的距离为 ,则该球的表面积为 .
,则该球的表面积为 . 与圆
与圆 交于不同的两点
交于不同的两点 若
若 ,
, 是坐标原点,那么实数
是坐标原点,那么实数 的取值范围是 .
的取值范围是 . 是圆的内接四边形,
是圆的内接四边形, ,过
,过 点的圆的切线与
点的圆的切线与 的延长线交于
的延长线交于 点,证明:
点,证明:


 .
. 在每段区间上的解析式,并在图中的直角坐标系中作出函数
在每段区间上的解析式,并在图中的直角坐标系中作出函数 对任意的实数
对任意的实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号