已知动点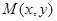 与定点
与定点 的距离和它到直线
的距离和它到直线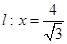 的距离之比是常数
的距离之比是常数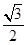 ,记
,记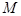 的轨迹为曲线
的轨迹为曲线 .
.
(I)求曲线 的方程;
的方程;
(II)设直线 与曲线
与曲线 交于
交于 两点,点
两点,点 关于
关于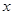 轴的对称点为
轴的对称点为 ,试问:当
,试问:当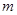 变化时,直线
变化时,直线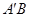 与
与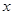 轴是否交于一个定点?若是,请写出定点的坐标,并证明你的结论;若不是,请说明理由.
轴是否交于一个定点?若是,请写出定点的坐标,并证明你的结论;若不是,请说明理由.
推荐套卷
已知动点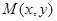 与定点
与定点 的距离和它到直线
的距离和它到直线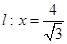 的距离之比是常数
的距离之比是常数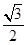 ,记
,记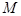 的轨迹为曲线
的轨迹为曲线 .
.
(I)求曲线 的方程;
的方程;
(II)设直线 与曲线
与曲线 交于
交于 两点,点
两点,点 关于
关于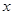 轴的对称点为
轴的对称点为 ,试问:当
,试问:当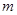 变化时,直线
变化时,直线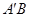 与
与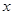 轴是否交于一个定点?若是,请写出定点的坐标,并证明你的结论;若不是,请说明理由.
轴是否交于一个定点?若是,请写出定点的坐标,并证明你的结论;若不是,请说明理由.