高中数学三面角、直三面角的基本性质试题

如果对数函数在上是减函数，则的取值范围是

A．

B．

C．

D．

已知为全集，,则（   ）

A．	B．
C．	D．

设，则使幂函数为奇函数且在上单调递增的a值的个数为(    )

A．0

B．1

C．2

D．3

已知椭圆的离心率为，为椭圆的左右焦点，；分别为椭圆的长轴和短轴的端点(如图) .若四边形的面积为.
（Ⅰ）求椭圆的方程.
（Ⅱ）抛物线的焦点与椭圆的右焦点重合，过点任意作一条直线，交抛物线于两点. 证明：以为直径的所有圆是否过抛物线上一定点.

下列函数中,在区间上是增函数的是  (  )

A．

B．

C．

D．

某商场销售某种商品的经验表明，该商品每日的销售量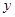（单位：千克）与销售价格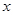（单位：元/千克）满足关系式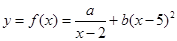，其中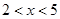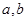，为常数，已知销售价格为4元/千克时，每日可销售出该商品5千克；销售价格为4.5元/千克时，每日可销售出该商品2.35千克.
（1）求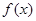的解析式；
（2）若该商品的成本为2元/千克，试确定销售价格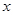的值，使商场每日销售该商品所获得的利润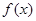最大.

设函数的定义域为，若存在非零实数满足，均有，且，则称为上的高调函数．如果定义域为的函数是奇函数，当时，，且为上的高调函数，那么实数的取值范围是（   ）

A．

B．

C．

D．

我国发射的“神舟六号”载人航天飞船的运行轨道是以地球的中心为一个焦点的椭圆，设其近地点A距地面为千米，远地点B距地面为千米，地球半径为千米，则飞船运行轨道的短轴长为（  ）

A．千米

B．千米

C．千米

D．千米

定义在R上的单调函数满足，且对任意都有

（I）试求的值并证明函数为奇函数；
（II）若对任意恒成立，求实数m的取值范围。

对于二次函数，
（1）指出图像的开口方向、对称轴方程、顶点坐标；
（2）画出它的图像，并说明其图像由的图像经过怎样平移得来；
（3）求函数的最大值或最小值；
（4）分析函数的单调性。

已知函数的图象与函数的图象恰有两个交点，则实数k的取值范围是_________.

当时，不等式恒成立，则实数的取值范围为  

已知函数满足。则=            

如图，公园有一块边长为2的等边△ABC的边角地，现修成草坪，图中把草坪分成面积相等的两部分，在上，在上.

（1）设，求用表示的函数关系式；
（2）如果是灌溉水管，为节约成本，希望它最短，的位置应在哪里？如果是参观线路，则希望它最长，的位置又应在哪里？请说明理由.

二次函数中，，则函数的零点个数是（   ）

A．0个

B．1个

C．2个

D．无法确定