定义在R上的函数f(x)的图象过点M(-6,2)和N(2,-6),对任意正实数k,有f(x+k)<f(x)成立,则当不等式|f(x-t)+2|<4的解集为(-4,4)时,实数t的值为________.
设f(x)和g(x)都是定义在同一区间上的两个函数,若对任意x∈[1,2],都有|f(x)+g(x)|≤8,则称f(x)和g(x)是“友好函数”,设f(x)=ax,g(x)= .
.
(1)若a∈{1,4},b∈{-1,1,4},求f(x)和g(x)是“友好函数”的概率;
(2)若a∈[1,4],b∈[1,4],求f(x)和g(x)是“友好函数”的概率.
已知函数f(x)是定义在R上的奇函数,当x<0时,f(x)=ex(x+1),给出下列命题:
①当x>0时,f(x)=ex(1-x);②函数f(x)有两个零点;③f(x)>0的解集为(-1,0)∪(1,+∞);④∀x1,x2∈R,都有|f(x1)-f(x2)|<2.
其中正确命题的个数是( )
| A.1 | B.2 |
| C.3 | D.4 |
已知函数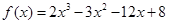 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若 ,求函数
,求函数 的值域.
的值域.
某公司一年需要一种计算机元件8000个,每天需同样多的元件用于组装整机,该元件每年分 次进货,每次购买元件的数量均为
次进货,每次购买元件的数量均为 ,购一次货需手续费500元.已购进而未使用的元件要付库存费,假设平均库存量为
,购一次货需手续费500元.已购进而未使用的元件要付库存费,假设平均库存量为 件,每个元件的库存费为每年2元,如果不计其他费用,请你帮公司计算,每年进货几次花费最小?
件,每个元件的库存费为每年2元,如果不计其他费用,请你帮公司计算,每年进货几次花费最小?
已知函数 ,
,
(1)若曲线 与
与 在公共点
在公共点 处有相同的切线,求实数
处有相同的切线,求实数 、
、 的值;
的值;
(2)当 时,若曲线
时,若曲线 与
与 在公共点
在公共点 处有相同的切线,求证:点
处有相同的切线,求证:点 唯一;
唯一;
(3)若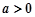 ,
, ,且曲线
,且曲线 与
与 总存在公切线,求正实数
总存在公切线,求正实数 的最小值
的最小值
(满分12分)设f (x) 是定义在 [-1,1] 上的偶函数,f (x) 与g(x) 的图象关于x =" 1" 对称,且当x Î [2,3] 时,g(x) = a (x-2)-2 (x-2) 3(a 为常数).
 (Ⅰ)求f (x) 的解析式;
(Ⅰ)求f (x) 的解析式;
(Ⅱ)若f (x) 在 [0,1] 上是增函数,求实数a 的取值范围;
(Ⅲ)若a  Î (-6,6),问能否使f (x) 的最大值为 4?请说明理由.
Î (-6,6),问能否使f (x) 的最大值为 4?请说明理由.
(满分12分)某专卖店销售一新款服装,日销售量(单位为件)f (n) 与时间n(1≤n≤30、nÎ N*)的函数关系如下图所示,其中函数f (n) 图象中的点位于斜率为 5 和-3 的两条直线上,两直线交点的横坐标为m,且第m天日销售量最大.
(Ⅰ)求f (n) 的表达式,及前m天的销售总数;
(Ⅱ)按以往经验,当该专卖店销售某款服装的总数超过 400 件时,市面上会流行该款服装,而日销售量连续下降并低于 30 件时,该款服装将不再流行.试预测本款服装在市面上流行的天数是否会超过 10 天?请说明理由.
