(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷
总体由编号为01,02,…,19,20的20个个体组成,利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
| 7816 6572 0802 6314 0702 4369 9728 0198 |
| 3204 9234 4935 8200 3623 4869 6938 7481 |
A.08 B.07 C.02 D.01
从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是( )
A.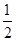 |
B.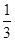 |
C.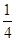 |
D.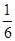 |
在样本的频率分布直方图中,共有11个小长方形,若中间一个长方形的面积等于其他10个小长方形面积和的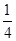 ,且样本容量为160,则中间一组的频数为( )
,且样本容量为160,则中间一组的频数为( )
| A.32 | B.0.2 | C.40 | D.0.25 |
某校为了研究学生的性别和对待某一活动的态度(支持和不支持的两种态度)的关系,运用2×2列联表进行独立性检验,经计算K2=7.069,则所得到的统计学结论是:有________的把握认为“学生性别与支持该活动有关系”( )
附:
| P(K2≥k0) |
0.100 |
0.050 |
0.025 |
0.010 |
0.001 |
| k0 |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
A.0.1% B.1% C.99% D.99.9%
某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况,从两块地各随机抽取了10株树苗,用茎叶图表示上述两组数据,对两块地抽取树苗的高度的平均数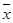 甲、
甲、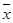 乙和中位数y甲、y乙进行比较,下面结论正确的是( )
乙和中位数y甲、y乙进行比较,下面结论正确的是( )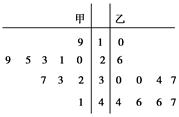
A.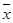 甲> 甲>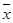 乙,y甲>y乙 乙,y甲>y乙 |
B.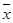 甲< 甲<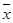 乙,y甲<y乙 乙,y甲<y乙 |
C.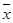 甲< 甲<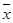 乙,y甲>y乙 乙,y甲>y乙 |
D.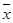 甲> 甲>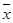 乙,y甲<y乙 乙,y甲<y乙 |
连续抛掷两枚正方体骰子(它们的六个面分别标有数字1,2,3,4,5,6),记所得朝上的面的点数分别为x,y,过坐标原点和点P(x,y)的直线的倾斜角为θ,则θ>60°的概率为( )
A.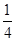 |
B.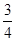 |
C.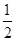 |
D.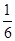 |
下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程 =3-5x,变量x增加一个单位时,y平均增加5个单位;
=3-5x,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程 =
=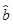 x+
x+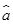 必过(
必过( ,
, );
);
④在一个2×2列联表中,由计算得K2=13.079,则有99%的把握确认这两个变量间有关系.
其中错误的个数是( )
本题可以参考独立性检验临界值表:
| P(K2≥k) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
A.0 B.1 C.2 D.3
由不等式组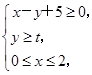 围成的三角形区域内有一个内切圆,向该三角形区域内随机投一个点,该点落在圆内的概率是关于t的函数P(t),则( )
围成的三角形区域内有一个内切圆,向该三角形区域内随机投一个点,该点落在圆内的概率是关于t的函数P(t),则( )
| A.P′(t)>0 | B.P′(t)<0 | C.P′(t)=0 | D.P′(t)符号不确定 |
甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则( )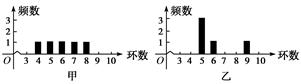
| A.甲的成绩的平均数小于乙的成绩的平均数 | B.甲的成绩的中位数等于乙的成绩的中位数 |
| C.甲的成绩的方差小于乙的成绩的方差 | D.甲的成绩的极差小于乙的成绩的极差 |
在区间[-π,π]内随机取两个数分别为a,b,则使得函数f(x)=x2+2ax-b2+π2有零点的概率为( )
A.1-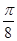 |
B.1-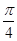 |
C.1-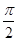 |
D.1-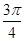 |
高三(1)班共有56人,学号依次为1,2,3,…,56,现用系统抽样的办法抽取一个容量为4的样本,已知学号为6,34,48的同学在样本中,那么还有一个同学的学号应为________.
右图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为[20.5,21.5),[21.5,22.5),[22.5,23.5),[23.5,24.5),[24.5,25.5),[25.5,26.5].已知样本中平均气温低于22.5 ℃的城市个数为11,则样本中平均气温不低于25.5 ℃的城市个数为________.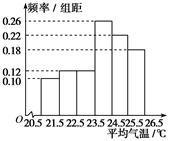
一个袋子中装有六个大小形状完全相同的小球,其中一个编号为1,两个编号为2,三个编号为3.现从中任取一球,记下编号后放回,再任取一球,则两次取出的球的编号之和等于4的概率是________.
右面茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为________.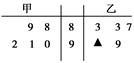
若从集合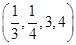 中随机抽取一个数记为a,从集合{-1,1,-2,2}中随机抽取一个数记为b,则函数f(x)=ax+b(a>0,a≠1)的图象经过第三象限的概率是________.
中随机抽取一个数记为a,从集合{-1,1,-2,2}中随机抽取一个数记为b,则函数f(x)=ax+b(a>0,a≠1)的图象经过第三象限的概率是________.
已知A、B、C三个箱子中各装有两个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2.现从A、B、C三个箱子中各摸出一个球.
(1)若用数组(x,y,z)中的x、y、z分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组(x,y,z)的所有情形,并回答一共有多少种;
(2)如果请您猜测摸出的这三个球的号码之和,猜中有奖.那么猜什么数获奖的可能性最大?请说明理由.
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.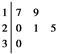
(1)根据茎叶图计算样本均值.
(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人?
(3)从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.
某高校组织自主招生考试,共有2 000名优秀同学参加笔试,成绩均介于195分到275分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成8组:第1组[195,205),第2组[205,215),…,第8组[265,275].如图是按上述分组方法得到的频率分布直方图,且笔试成绩在260分(含260分)以上的同学进入面试.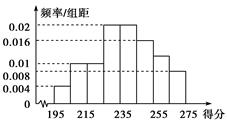
(1)估计所有参加笔试的2 000名同学中,参加面试的同学人数;
(2)面试时,每位同学抽取两个问题,若两个问题全答错,则不能取得该校的自主招生资格;若两个问题均回答正确且笔试成绩在270分以上,则获A类资格;其他情况下获B类资格.现已知某中学有两人获得面试资格,且仅有一人笔试成绩为270分以上,在回答两个面试问题时,两人对每一个问题正确回答的概率均为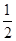 ,求恰有一名同学获得该高校B类资格的概率.
,求恰有一名同学获得该高校B类资格的概率.
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数如下表:
| |
1号 |
2号 |
3号 |
4号 |
5号 |
| 甲组 |
4 |
5 |
x |
9 |
10 |
| 乙组 |
5 |
6 |
7 |
y |
9 |
(1)已知两组技工在单位时间内加工的合格零件平均数为7,分别求出甲、乙两组技工在单位时间内加工的合格零件的方差,并由此分析两组技工的加工水平;
(2)质检部门从该车间甲、乙两组中各随机抽取一名技工,对其加工的零件进行检测,若2人加工的合格零件个数之和超过14,则称该车间“质量合格”,求该车间“质量合格”的概率.
甲、乙两所学校高三年级分别有1 200人,1 000人,为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
| 分组 |
[70,80) |
[80,90) |
[90,100) |
[100,110) |
| 频数 |
3 |
4 |
8 |
15 |
| |
|
|
|
|
| 分组 |
[110,120) |
[120,130) |
[130,140) |
[140,150] |
| 频数 |
15 |
x |
3 |
2 |
乙校:
| 分组 |
[70,80) |
[80,90) |
[90,100) |
[100,110) |
| 频数 |
1 |
2 |
8 |
9 |
| |
|
|
|
|
| 分组 |
[110,120) |
[120,130) |
[130,140) |
[140,150] |
| 频数 |
10 |
10 |
y |
3 |
(1)计算x,y的值;
(2)若规定考试成绩在[120,150]内为优秀,请分别估计两所学校数学成绩的优秀率;
(3)由以上统计数据填写下面的2×2列联表,并判断能否在犯错误的概率不超过0.10的前提下认为两所学校的数学成绩有差异.
| |
甲校 |
乙校 |
总计 |
| 优秀 |
|
|
|
| 非优秀 |
|
|
|
| 总计 |
|
|
|
参考数据与公式:由列联表中数据计算K2=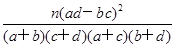 .
.
临界值表
| P(K2≥k0) |
0.10 |
0.05 |
0.010 |
| k0 |
2.706 |
3.841 |
6.635 |
 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号