(12分)已知函数
（1）在给定的直角坐标系内画出
的图象；
（2）写出的单调递增区间（不需要证明）；
（3）写出的最大值和最小值（不需要证明）．
广东某品牌玩具企业的产品以往专销欧州市场，在欧债危机的影响下，欧州市场的销量受到严重影响，该企业在政府的大力扶助下积极开拓国内市场，主动投入内销产品的研制开发，并基本形成了市场规模，自2010年9月以来的第n个月（2010年9月为每一个月），产品的内销量、出口量和销售总量（内销量与出口量的和）分别为bn、cn和an（单位万件），分析销售统计数据发现形成如下营销趋势：bn＋1＝aan，cn＋1＝an＋ba
（其中a、b为常数），且a1＝1万件，a2＝1.5万件，a3＝1.875万件.
（1）求a,b的值，并写出an＋1与an满足的关系式；
（2）如果该企业产品的销售总量an呈现递增趋势，且控制在2万件以内，企业的运作正常且不会出现资金危机；试证明：an＜an＋1＜2.
（3）试求从2010年9月份以来的第n个月的销售总量an关于n的表达式.
(本题满分16分)
设
为实数，且
（1）求方程
的解；
（2）若
，
满足
，试写出与的等量关系（至少写出两个）；
（3）在（2）的基础上，证明在这一关系中存在满足
.
(本小题满分14分)
已知二次函数
满足：
，
，且该函数的最小值为1.
⑴ 求此二次函数的解析式;
⑵ 若函数的定义域为
= 
.(其中
). 问是否存在这样的两个实数
,使得函数的值域也为?若存在,求出的值;若不存在,请说明理由.
解答题：本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤.
16、（本题共两小题，每小题6分，共12分）
（1）求值：
(本小题满分12分)
函数
的定义域为[－1,2]，
（1）若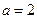
，求函数
的值域；
（2）若
为非负常数，且函数是[－1,2]上的单调函数，求的范围及函数的值域。
(本题8分)某民营企业生产A，B两种产品，根据市场调查和预测，A产品的利润与投资成正比，其关系如图1，B产品的利润与投资的算术平方根成正比，其关系如图2（注：利润与投资单位是万元）
（1）分别将A，B两种产品的利润表
示为投资的函数，并写出它们的函数关系式
（2）该企业已筹集到10万元资金，并全部投入A，B两种产品的生产，问：怎样分配这10万元投资，才能是企业获得最大利润，其最大利润约为多少万元（精确到1万元）.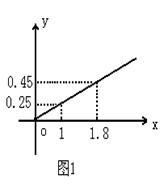
（本小题满分12分）已知某种稀有矿石的价值
（单位：元）与其重量
（单位：克）的平方成正比，且
克该种矿石的价值为
元。
⑴写出（单位：元）关于（单位：克）的函数关系式；
⑵若把一块该种矿石切割成重量比为
的两块矿石，求价值损失的百分率；
⑶把一块该种矿石切割成两块矿石时，切割的重量比为多少时，价值损失的百分率最大。（注：价值损失的百分率
；在切割过程中的重量损耗忽略不计）
如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN，要求 
在 
上，N在AD上，且对角线MN过C点，已知AB＝4米，AD＝3米，设AN的长为x米（x >3）。
（1） 要使矩形AMPN的面积大于54平方米，则AN的长应在什么范围内？
（2） 求当AM、AN的长度是多少时，矩形花坛AMPN的面积最小？并求出最小面积．
（本小题满分12分）
某地区上年度电价为0.8元/kW·h，年用电量为akW·h，本年度计划将电价降到0.55元/kW·h至0.75元/kW·h之间，而用户期望电价为0.4元/kW·h，经测算，下调电价后新增的用电量与实际电价和用户期望电价的差成反比（比例系数为k）．该地区电力的成本价为0.3元/kW·h．
(Ⅰ)写出本年度电价下调后，电力部门的收益y与实际电价x的函数关系式；
(Ⅱ)设k=0.2a，当电价最低定为多少时仍可保证电力部门的收益比上年至少增长20%？
（注：收益=实际用电量×(实际电价-成本价)）
(本小题满分12分)
. 设
R, 且
, 定义在区间
内的函数
是奇函数.
（Ⅰ）求
的取值范围;
（Ⅱ）讨论函数
的单调性，并加以证明.
（本题8分）某村计划建造一个室内面积为800
的矩形蔬菜温室。在温室内，沿左．右两侧与后侧内墙各保留1
宽的通道，沿前侧内墙保留3宽的空地，当矩形温室的边长各为多少时，蔬菜的种植面积最大？最大种植面积是多少？
（本小题满分12分）
某汽车公司购买了4辆大客车，每辆200万元，用于长途客运，预计每辆车每年收入约100万元，每辆车每年各种费用约为16万元，且从第二年开始每年比上一年所需费用要增加16万元．
（1）写出4辆车运营的总利润
（万元）与运营年数
的函数关系式；
（2）这4辆车运营多少年，可使年平均运营利润最大？
粤公网安备 44130202000953号
.
是
上的增函数
取得最小值？证明你的结论；
数，求a的取值范围。