高中数学多面角及多面角的性质填空题

已知函数，下列命题中正确的是            （写出所有正确命题的序号）
①的周期为；
②的图象关于点对称；
③在（）上单调递增；  
④在（）上有3个零点．

已知函数f（x）=sinx+cosx，则下列命题正确的是   ．（填上你认为正确的所有命题的序号）
①函数f（x）（x∈[0, ]）的单调递增区间是[0, ]；
②函数f（x）的图像关于点（－，0）对称；
③函数f（x）的图像向左平移m（m>0）个单位长度后，所得的图像关于y轴对称，则m的最小值是；
④若实数m使得方程f（x）＝m在[0,2]上恰好有三个实数解x₁,x₂,x₃，则x₁＋x₂＋x₃＝．

给出下列五个命题：
①函数的一条对称轴是；
②函数的图象关于点（,0）对称；
③正弦函数在第一象限为增函数；
④若，则，其中；
⑤函数的图像与直线有且仅有两个不同的交点，则的取值范围为.
以上五个命题中正确的有            （填写所有正确命题的序号）

已知为锐角，，则________．

设函数满足，当时，．则       .

如图所示，点是函数图象的最高点，、是图象与轴的交点，若，则=          ．

若，则函数的最大值是___________．

已知函数，则的最大值为    ．

下列结论中：
1）函数为奇函数
2）函数的图像关于点对称
3）函数的图像的一条对称轴为
4）若，则 
其中正确的结论序号为____________________．

已知，，在曲线与直线=1的交点中，
若相邻交点距离的最小值为，则的最小正周期为_________．

已知cos（α+）=，求sin（﹣α）的值      ．

已知，为锐角，则      ，    ．

下面有五个命题：
①函数的最小正周期是；
②终边在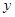轴上的角的集合是；
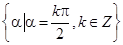③函数，在区间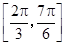上是增函数；
④若动直线与函数和的图像分别交于两点，则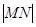的最大值为1．
其中真命题的序号是           。

关于函数f（x）＝cos＋cos，有下列说法：
①y＝f（x）的最大值为；
②y＝f（x）是以π为最小正周期的周期函数；
③y＝f（x）在区间上单调递减；
④将函数y＝cos 2x的图象向左平移个单位后，将与已知函数的图象重合．
其中正确说法的序号是________．（注：把你认为正确的说法的序号都填上）

（，，为常数，，，）的图象如图所示，则的值为      ．