高中数学多面角及多面角的性质试题

函数的部分图象如图所示，若将的图象向右平移个单位后，得到的图象关于原点对称，则的最小值为（   ）

A．

B．

C．

D．

已知函数）图象的一部分如图所示．

（1）求函数的解析式；
（2）设，求的值.

已知函数的图象与直线的三个相邻交点的横坐标分别为2,4,8，则的单调递增区间是（    ）

A．

B．

C．

D．无法确定

已知如图是函数y=2sin（ωx+φ）（|φ|＜）的图象，那么（ ）

A．ϖ=，φ=

B．ϖ=，φ=﹣

C．ϖ=2，φ=

D．ϖ=2，φ=﹣

已知函数（）的最大值为，最小值为．
（1）求，的值；
（2）求当时，函数的值域．

已知函数的最小正周期为，则在区间上的值域为（  ）

A．	B．
C．	D．

已知函数①，②，则下列结论正确的是（  ）

A．两个函数的图象均关于点成中心对称

B．函数①的图象的纵坐标伸长为原来的倍，横坐标缩小为原来的，再向左平移个单位即得②的图象

C．两个函数在区间上都是单调递增函数

D．两个函数的最小正周期相同

设向量＝，＝，其中，,已知函数·的最小正周期为．
（Ⅰ）求的值；
（Ⅱ）若是关于的方程的根，且，求的值．

已知简谐运动的图象经过点，则该简谐运动的最小正周期和初相分别为（   ）

A．，

B．，

C．，

D．，

的值为（  ）

A．－

B．

C．

D．－

已知函数 $f\left(x\right)=A\sin (3x+\phi )(A＞0,x\in (-\infty ,+\infty ),0＜\phi ＜\pi ）$ 在x= $x=\frac{\mathrm{\pi }}{12}$ 时取得最大值4．．
（1）求 $f\left(x\right)$ 的最小正周期；
（2）求 $f\left(x\right)$ 的解析式；
（3）若 $f(\frac{2}{3}\alpha +\frac{\mathrm{\pi }}{12})=\frac{12}{5}$ ．求 $\tan 2\alpha$ 的值．

已知函数f（x）=asinωxcosωx+cos²ωx（a＞0，ω＞0）的最小正周期为，最小值为﹣，将函数f（x）的图象向左平移φ（φ＞0）个单位后，得到的函数图象的一条对称轴为x=，则φ的值不可能为（ ）

A．

B．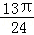

C．

D．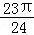

已知函数f（x）=sinxcosx﹣cos²x．
（1）求f（x）的最小正周期；
（2）求f（x）在区间上的最小值，并求取得最小值时x的值．

如图是函数的图象的一部分,则=（  ）

A．1	B．
C．	D．

设函数，则的最小正周期为（  ）

A．

B．

C．

D．