高中数学多面角及多面角的性质试题

下列命题，正确的个数是（  ）
①直线是函数图像的一条对称轴；
②将函数的图像上的每个点的横坐标缩短为原来的（纵坐标不变），再向左平移个单位长度，得到函数的图像；
③设随机变量，若，则；
④的二项展开式中含有项的二项式系数是210．

A．1

B．2

C．3

D．4

函数的单调增区间为（   ）

A．	B．
C．	D．

将函数的图象向右平移个单位长度后得到函数的图象，的图象都经过点，则的值不可能是（ ）

A．

B．

C．

D．

将函数f（x）=sin2x的图象向右平移φ（0＜φ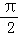＜）个单位后得到函数g（x）的图象．若对满足|f（x₁）﹣g（x₂）|=2的x₁、x₂，有|x₁﹣x₂|_min=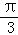，则φ=（ ）

A．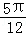

B．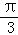

C．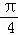

D．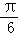

函数y=的单调递减区间为           ．

函数f（x）=sinπx+cosπx+|sinπx﹣cosπx|对任意x∈R有f（x₁）≤f（x）≤f（x₂）成立，则|x₂﹣x₁|的最小值为       ．

函数的部分图象如图所示，若将的图象向右平移个单位后，得到的图象关于原点对称，则的最小值为（   ）

A．

B．

C．

D．

已知函数f（x）=1+sinxcosx．
（1）求函数f（x）的最小正周期和单调递减区间；
（2）若tanx=2，求f（x）的值．

已知函数）图象的一部分如图所示．

（1）求函数的解析式；
（2）设，求的值.

已知函数 $f\left(x\right)=A\sin (3x+\phi )(A＞0,x\in (-\infty ,+\infty ),0＜\phi ＜\pi ）$ 在x= $x=\frac{\mathrm{\pi }}{12}$ 时取得最大值4．．
（1）求 $f\left(x\right)$ 的最小正周期；
（2）求 $f\left(x\right)$ 的解析式；
（3）若 $f(\frac{2}{3}\alpha +\frac{\mathrm{\pi }}{12})=\frac{12}{5}$ ．求 $\tan 2\alpha$ 的值．

已知函数f（x）=asinωxcosωx+cos²ωx（a＞0，ω＞0）的最小正周期为，最小值为﹣，将函数f（x）的图象向左平移φ（φ＞0）个单位后，得到的函数图象的一条对称轴为x=，则φ的值不可能为（ ）

A．

B．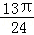

C．

D．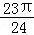

已知函数f（x）=sinxcosx﹣cos²x．
（1）求f（x）的最小正周期；
（2）求f（x）在区间上的最小值，并求取得最小值时x的值．

如图是函数的图象的一部分,则=（  ）

A．1	B．
C．	D．

设函数，则的最小正周期为（  ）

A．

B．

C．

D．

已知函数的图象与轴交于点P、与轴的相邻两个交点记为A、B，若的面积等于，则＝________．