高中数学多面角及多面角的性质试题

已知，⑴求的值；⑵求的值．

已知函数
（1）求函数的最大值和最小值以及取最大、最小值时相应的取值集合；
（2）写出函数的单调递增区间．
（3）作出此函数在一个周期内的图像。

如图，摩天轮的半径为40m，摩天轮的圆心O距地面的高度为50m，摩天轮做匀速转动，每3min转一圈，摩天轮上的点P的起始位置在最低点处．
（1）已知在时刻t (min)时点P距离地面的高度为f (t) = A sin + h，求2006min时点距离地面的高度．
（2）求证：不论t为何值，f (t) + f (t + 1) + f (t + 2)是定值．

已知函数f(x)＝2sin x(sin x＋cos x)．
(1)求函数f(x)的最小正周期和最大值；
(2)在给出的平面直角坐标系中，画出函数y＝f(x)在区间上的图象．

已知函数 $f\left(x\right)=A\sin (3x+\phi )(A＞0,x\in (-\infty ,+\infty ),0＜\phi ＜\pi ）$ 在x= $x=\frac{\mathrm{\pi }}{12}$ 时取得最大值4．．
（1）求 $f\left(x\right)$ 的最小正周期；
（2）求 $f\left(x\right)$ 的解析式；
（3）若 $f(\frac{2}{3}\alpha +\frac{\mathrm{\pi }}{12})=\frac{12}{5}$ ．求 $\tan 2\alpha$ 的值．

已知函数f（x）=asinωxcosωx+cos²ωx（a＞0，ω＞0）的最小正周期为，最小值为﹣，将函数f（x）的图象向左平移φ（φ＞0）个单位后，得到的函数图象的一条对称轴为x=，则φ的值不可能为（ ）

A．

B．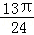

C．

D．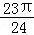

已知函数f（x）=sinxcosx﹣cos²x．
（1）求f（x）的最小正周期；
（2）求f（x）在区间上的最小值，并求取得最小值时x的值．

如图是函数的图象的一部分,则=（  ）

A．1	B．
C．	D．

设函数，则的最小正周期为（  ）

A．

B．

C．

D．

已知函数的图象与轴交于点P、与轴的相邻两个交点记为A、B，若的面积等于，则＝________．

已知，，则            ．

函数的最大值是            ．

(本小题满分14分)
已知函数，点分别是函数图象上的最高点和最低点．
（1）求点的坐标以及的值；
（2）设点分别在角的终边上，求的值．

已知函数f(x)＝2sin(2x＋φ)(0＜φ＜2π)的图象过点(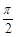，－2)．
（1）求φ的值；
（2）若f(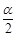)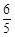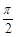＝，－＜α＜0，求sin(2α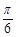－)的值．

已知函数，求：
（1）函数的最小正周期；（2）函数的最大值及对应自变量的集合。