(本小题满分12分)已知函数 ,
,
(Ⅰ)求函数 的周期及单调递增区间;
的周期及单调递增区间;
(Ⅱ)在 中,三内角
中,三内角 ,
, ,
, 的对边分别为
的对边分别为 ,已知函数
,已知函数 的图象经过点
的图象经过点 成等差数列,且
成等差数列,且 ,求
,求 的值.
的值.
已知函数 ,给出下列四个命题:
,给出下列四个命题:
①若 ,则
,则 ; ②
; ② 的最小正周期是
的最小正周期是 ;
;
③ 在区间
在区间 上是增函数; ④
上是增函数; ④ 的图象关于直线
的图象关于直线 对称
对称
| A.①②④ | B.①③ | C.②③ | D.③④ |
已知函数 (
( )的最小正周期为
)的最小正周期为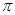 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)将函数 的图象向左平移
的图象向左平移 个单位,再向上平移
个单位,再向上平移 个单位,得到函数
个单位,得到函数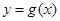 的图象.若
的图象.若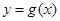 在
在 上至少含有
上至少含有 个零点,求
个零点,求 的最小值.
的最小值.
已知函数
在x=
时取得最大值4..
(1)求
的最小正周期;
(2)求
的解析式;
(3)若
.求
的值.
已知函数f(x)=asinωxcosωx+ cos2ωx(a>0,ω>0)的最小正周期为
cos2ωx(a>0,ω>0)的最小正周期为 ,最小值为﹣
,最小值为﹣ ,将函数f(x)的图象向左平移φ(φ>0)个单位后,得到的函数图象的一条对称轴为x=
,将函数f(x)的图象向左平移φ(φ>0)个单位后,得到的函数图象的一条对称轴为x= ,则φ的值不可能为( )
,则φ的值不可能为( )
A. |
B.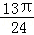 |
C. |
D.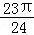 |
已知函数f(x)=sinxcosx﹣cos2x.
(1)求f(x)的最小正周期;
(2)求f(x)在区间 上的最小值,并求取得最小值时x的值.
上的最小值,并求取得最小值时x的值.
已知函数
 的图象与
的图象与 轴交于点P、与
轴交于点P、与 轴的相邻两个交点记为A、B,若
轴的相邻两个交点记为A、B,若 的面积等于
的面积等于 ,则
,则 =________.
=________.
已知函数f(x)=2sin(2x+φ)(0<φ<2π)的图象过点(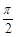 ,-2).
,-2).
(1)求φ的值;
(2)若f(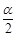 )=
)=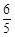 ,-
,-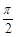 <α<0,求sin(2α-
<α<0,求sin(2α-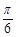 )的值.
)的值.