如图，摩天轮的半径为40m，摩天轮的圆心O距地面的高度为50m，摩天轮做匀速转动，每3min转一圈，摩天轮上的点P的起始位置在最低点处．
（1）已知在时刻t (min)时点P距离地面的高度为f (t) = A sin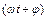 
+ h，求2006min时点距离地面的高度．
（2）求证：不论t为何值，f (t) + f (t + 1) + f (t + 2)是定值．
相关试题
,若
.
的面积为
,求函数
的单调增区间
.
的最小正周期和值域;
为第二象限角，且
,求
的值.
在
处取得极值
.
;
为R上的奇函数,求函数
在区间
上的极值.
为平面向量,
.
的值;
,求实数
的值.
为圆
的直径，点
、
在圆
，矩形
所在的平面和圆
，
.
平面
；
的中点为
，求证：
平面
；
分成的两个锥体的体积分别为
，
，求
．相关知识点
推荐套卷
如图，摩天轮的半径为40m，摩天轮的圆心O距地面的高度为50m，摩天轮做匀速转动，每3min转一圈，摩天轮上的点P的起始位置在最低点处．
（1）已知在时刻t (min)时点P距离地面的高度为f (t) = A sin 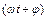+ h，求2006min时点距离地面的高度．
（2）求证：不论t为何值，f (t) + f (t + 1) + f (t + 2)是定值．
粤公网安备 44130202000953号